Qui és l'intrús?

Una de les taques amb més èxit durant les trobades de formació de mestres són les QUELIs. Els mestres de seguida veuen el seu potencial per fer parlar als alumnes i intueixen com s'engrescaran els alumnes buscant arguments per defensar les seves respostes. O sigui, les QUELIs són tasques ideals per valorar les dimensions "comunicació i represantació" i "raonament i prova".

Què són les QUELIs?
Per explicar què significa QUELIs o WODB i quines característiques tenen aquestes tasques, per comentar com podem portar-les a l'aula i quines variants hi ha creiem que el millor es remitir-vos al resum de la presentació que van fer @davidobrador i @ccbcnmvd al C2EM 2016:

Exemples de QUELI's
Hi ha exemples per a totes les edats i relacionades amb tots els blocs temàtics. A més de la pàgina "oficial" que recull exemples d'aquestes tasques: http://wodb.ca, a Twitter, sota l'etiqueta #wodb els usuaris comparteixen les que dissenyen ells i les que proposen en les seves aules:

Comentarem la nostra experiència amb tres QUELIs de geometria que vam portar a l'aula

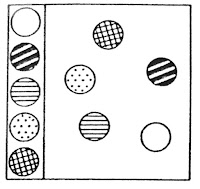
Anomenarem A a l'objecte que està a dalt a l'esquerra, B el que està a dalt a la dreta, C el que està a baix a l'esquerra i D a l'últim

Amb aquesta proposta surten arguments relacionats amb

• els eixos de simetria: B és l'intrús perquè és l'únic que les diagonals són eixos de simetria o C és l'intrús perquè és l'únic que té un únic eix de simetria o D és l'intrús perquè és l'únic que no té cap eix de simetria  
• les diagonals: A és l'intrús perquè és l'únic que té les diagonals iguals tallant-se al punt mig o  és l'intrús perquè és l'únic que té diagonals perpendiculars o C és l'intrús perquè és l'únic que les diagonals no es tallen al punt mig
• els costats: C és l'intrús perquè és l'únic que té tres costats de mides diferents o A és l'intrús perquè és l'únic que té costats perpendiculars o B és l'intrús perquè és l'únic que té tots els costats igual
• els angles: A és l'intrús perquè és l'únic que té tots els angles iguals o C és l'intrús perquè és l'únic que té un angle obtús oposat a un angle agut
• ... 

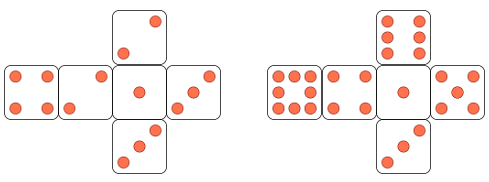
Aquí també els arguments han estat variats

• A és l'intrús perquè és l'únic acutangle, o l'únic que té com a eix de simetria la diagonal del geoplà
• B és l'intrús perquè és l'únic escalè, o l'únic que té un costat de longitud major que 4
• C és l'intrús perquè és l'únic rectangle o l'únic que la seva frontera només té contacte amb tres punts del geoplà
• D és l'intrús perquè és l'únic que no té punts del geoplà a l'nterior, o l'únic que té un costat de longitud 4

En aquest cas, a més de convidar als alumnes a exposar arguments sobre perquè cadascuna de les figures era "l'intrusa" vam plantejar que pensessin què tenien en comú les peces vermelles, les verdes i sobre tot les blaves. El fet de reconeixer que el mateix color indicava mateixa àrea els va donar nous arguments: C és l'intrús perquè és l'únic que té àrea 9 triangles verds o D és l'intrús perquè és l'únic que té àrea 8 triangles verds.

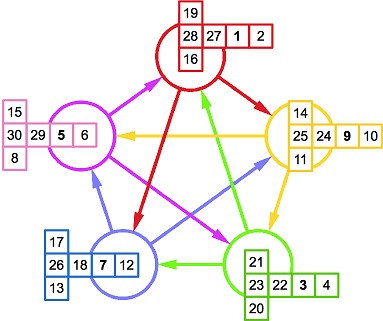
A la fase final del Fem Matemàtiques 2019 l'organització va proposar als participants com a activitat inicial per formar grups puzzles relacionats amb #QUELIs (a cada participant es lliurava amb la inscripció una imatge que corresponia a la cinquena part d'una imatge major que corresponia a una tasca del tipus "qui és l'intrús?" havien de juntar-se amb la resta de participants que tenien imatges de la mateixa QUELI i entre tots argumentar les quatre opcions)

Freqüència de lletres

Creiem que les llengues són un context pertinent i interessant per fer estadística a l'aula:

Podem estudiar els noms dels alumnes

• llargària

En aquestes dues fotografies apareixen els alumnes de #eso1sdk (curs 16-17) que també van estudiar els noms dels alumnes d'altres grups de l'escola (cada petit grup d'alumnes de 1r d'ESO va estudiar una classe) donant lloc als següents dos gràfics:

• lletra inicial

• lletra final

Respecte a l'anàlisi de la lletra final dels noms trobem molt interessant aquest gràfic

http://www.prooffreader.com/2014/04/baby-names-rise-of-n.html

També podem estudiar la freqüència d'aparició de vocals en texts escrits en diferents llengües.

En aquest vídeo gravat durant la sessió dedicada a l'Estadística en el mòdul 2 del curs ARAMAT vam exemplificar com fer aquest estudi:

Aquest vídeo de la col·lecció Videomat també tracta aquest tema:

El @Simon_Gregg va proposar als seus alumnes analitzar la freqüència de totes les lletres basant-se en una proposta de @mburnsmath

El detonant per escriure avui aquest post que fa molt que teníem en ment és aquest interessant fil trobat a Twitter on @eliasmgf, professor de llengua castellana, vol justificar en base a la freqüencia de les lletres la norma ortogràfica: "Las palabras agudas (no monosílabas) se acentúan si terminan en vocal, ene o ese". La base de la seva argumentació és el gràfic de "distribución de las letras dentro de las palabras del español" malgrat que aquí les freqüencies no són absolutes.

Comentari final:

En aquest post estem interessats en "lletres" per això hem esmentat l'estudi de la quantitat de lletres o de les lletres inicials i finals dels noms de persones. Però els noms de persones poden ser un motiu d'estudi per si mateixos. 

En aquest sentit, trobem interessant un article de diario.es sobre noms tradicionals vs moderns on apareixen aquests gràfics:

Un altre material per treballar la probabilitat

Complementant la sèrie d'entrades que ja vam dedicar a materials manipulatius per treballar la probabilitat avui parlarem d'un "artefacte" que coneixíem des de que el vam veure dins de la Caixa de Varga però sobre el qual no havíem parat atenció encara.

Es tracta d'una capseta de plàstic on hi ha una sèrie de boletes de diferents colors que apareixen alineades i no es poden moure i la mateixa quantitat de boles (i dels mateixos colors) que es mouen lliurement per la capseta. Al llibre "Combinatoire, statistiques et probabilités de 6 à 14 ans" de T. Varga i M. Dumont (1973) podem veure un dibuix i un petita anàlisi de l'artefacte i de les possibles coincidències quan alineem les boles lliures al costat de les fixes.

Comenten la temptació de pensar que la probabilitat de tenir k coincidències es representa així:

quan en realitat la probabilitat de que hi hagi 5 coincidència, malgrat que petita, és major que la probabilitat de que n'hi hagi 4, que és 0. Aquesta reflexió és extensible a altres quantitats de boles (n) ja que 1/n! = P(k=n) > P(k=n-1) = 0.

En realitat, la probabilitat de tenir k coincidències quan n= 5 es representa així:

En veure aquest gràfic ens ha sorprès que la diferència major en comparació al que proposàven Varga i Dumont com a "intuitiu" no és tant al voltant dels valors 4 i 5 com dels valors 0 i 1. Això es pot apreciar millor en analitzar la representació anterior per a altres quantitats de boles (n variant de 2 a 10)

Representació de la variació de la probabilitat de tenir k coincidències en els casos n=1 a n=10

Es així que ens hem preguntat quina relació hi ha entre P(k=0) i P(k=1) per a diferents valors de n i hem vist que:

• P(k=0) < P(k=1) quan n és senar i P(k=0) > P(k=1) 
• la diferència entre les dues probabilitats és 1/n!

Aquestes conclusions deriven de les dades següents:

• A000166 llista de valors donada per l'OEIS per als desarranjaments, o sigui, permutacions en les quals cap dels elements del conjunt no apareix en la seva posició original
• A000240 llista de valors donada per l'OEIS per a les permutacions que tenen un únic element del conjunt que apareix en la seva posició original
• R(n,k) és el nombre de permutacions de n elements en què exactament k elements estan en les seves posicions originals (desarranjaments parcials).

En el joc "Cursa de probabilitat" de la Caixa de Varga apareixen quatre targetes relacionades amb aquest artefacte (n=6):

Font: Perímetre

L'artefacte ofereix la possibilitat d'afegir uns trossets de plàstic que limiten la llibertat de moviment de les boles lliures i que amplien la possibilitat de proposar preguntes de probabilitat

Altres materials per treballar la probabilitat

Amb aquesta entrada donem per acabada una sèrie que hem estat desenvolupant en les últimes setmanes sobre materials manipulatius per treballar la probabilitat. Fins ara hem comentat tres materials:

• boles i urnes
• monedes
• daus

Avui comentarem altres materials:

Cartes
Els simuladors virtuals donen l'oportunitat de repetir un experiment moltíssims cops i també permeten projectar un experiment perquè sigui visualitzat simultàniament per tots els alumnes d'una classe. Entre els molts simuladors que ofereix el Manuel Sada en la seva pàgina web destaquem un sobre les cartes: Sacando cartas de una baraja 

Les baldufes de la Caixa de Varga

Baldufes

Tenim diversos simuladors del funcionament d'aquest material (per exemple, aquest) però volem destacar la importància de construir versions casolanes dels materials quan no els tenim disponibles, com les que tenim a l'Espai Jordi Esteve.

Quan afegim nombres a les regions de les baldufes podem ampliar el repertori d'experiments per fer amb elles. Un exemple d'aquests experiments el trobem a la proposta Which Spinners? del projecte Nrich

Exemple de l'applet que inclou la proposta Which Spinners? on es registra la suma de tres baldufes una de 3 zones, una de 4 i una de 9

Al blog de @Simon_Gregg trobareu una activitat preciosa que va fer a Primària: La millor i la pitjor baldufa

http://y4atist.blogspot.fr/2015/11/best-and-worst-spinners.html

Xinxetes

Encara que no sigui un material estàndard per treballar conceptes de probabilitat, a l'ARC ens proposen una interessant activitat sobre aquest tema amb aquest material: Com cau una xinxeta?  

Vídeo de l'activitat

Peces de dòmino

Un altre material no estàndard però que dóna molt de joc per treballar la probabilitat són les peces del dòmino. Un material per al qual les taules de doble entrada no determinen l'espai mostral tal com ho feien en el cas del llançament de dos daus. 

No  només hi ha dòminos de 28 peces, el de les peces que apareixen en aquesta foto té fins a 9 punts en cada quadre i el nombre de peces augmenta a 55. Font: http://commons.wikimedia.org

Què és més probable extreure una peça amb dos nombres iguals o una peça on hagi algun 6? Quina és la probabilitat de que la diferència de punts entre els dos quadres d'una peça sigui 3? Quina és la probabilitat que la suma de punts d'una peça sigui múltiple de 3?

Com a cloenda només podem dir que creiem que el treball amb probabilitat ha de passar per tres etapes fonamentals: 

• predicció del resultat d'un experiment
• experimentació amb materials manipulatius (complementada en els casos en que sigui possible amb la simulació virtual)
• confrontació de la predicció amb els resultats de l'experimentació i redacció de les conclusions extretes d'aquesta confrontació  

Materials per treballar la probabilitat: daus

Un dau
Per començar el tema recomanem llegir la introducció que fa el Joan Jareño a la seva proposta "Tirem els daus" on comenta la història i diferents tipus de daus. Destaquem altres dos apartats d'aquesta proposta:

• "Un dau carregat" on analitza com es pot saber quin nombre és afavorit per aquesta deformació.
• "Per què no em surt el cinc?" on analitza les ratxes de "mala sort"

En la sessió "Ell@s tienen la palabra" que des de fa un any escriu el PuntMat a la revista SUMA (Nº 73, pp 89-98) vam presentar una activitat per fer amb un dau. Es tracta d'una adaptació del joc "La ciutat fantasma" de la Caixa de Varga que es juga sobre aquest tauler

Se coloca una ficha en la casilla indicada como "salida" y se lanza un dado dos veces. en cada ocasión, si sale 1, 2 o 3, se avanza una casilla y se sube otra. Pero si sale 4, 5 o 6, se avanza una casilla y se baja otra. Después de introducir el juego es momento de que conjeturen, experimenten y tomen la palabra para discutir: ¿en qué casillas puede acabar el recorrido?, ¿en cuál de ellas es más probable que acabe? Si hacemos el experimento unas 900 veces, ¿cuántas veces cabe esperar que acabe en cada una de las casillas? Es interesante analizar cómo afecta a las respuestas anteriores el hecho de realizar pequeños cambios en las reglas del juego. Para ello planteemos una segunda versión de éste: sólo cambia que avanzo una casilla y subo una casilla cuando en el dado sale 1, pero si sale cualquier otro número después de avanzar una casilla, bajo una. en esta nueva versión del juego, las casillas en las que puede acabar el recorrido son las mismas (F, H y J) pero ahora la más probable ya no es la H, sino la J.

Una tercera versió d'aquest joc passa per avançar una casella i pujar-ne una altra quan al dau surt un 1 o un 2 i avançar una casella i baixar-ne una altra quan surt  un 3, un 4, un 5 o un 6. En aquest cas és igualment probable acabar el recorregut en la casella H o en la J (4 entre 9 en cada cas). Encara que hi ha una certa probabilitat d'acabar el recorregut en la casella F (1 entre 9) però no es lògic apostar per acabar allí a menys que el premi compensi el risc. Podem proposar als alumnes que reflexionin sobre les raons per les que continuaria sent poc raonable apostar per la casella F encara que el premi per encertar quan s'aposta per la casella F és el doble (o, fins i tot, el triple) que quan s'aposta per les caselles H o J. 

Aquesta idea de canviar els premis per equilibrar jocs en els quals els resultats no són igualment probables també ha estat explorada en algunes de les activitats del Proyecto Gauss. Un exemple molt interessant en aquest sentit és el de la "Ruleta de Frutas" que estudia a quin preu s'ha de cobrar el dret a jugar els organitzadors si no volen perdre diners.

Dos daus

A l'article de SUMA esmentat abans vam desenvolupar un joc que ben podria formar part del post anterior: Parells i senars. 

Tenemos muchas situaciones en la que dos niños deben repartirse dos tareas una de las cuales es la preferida por ambos, en esos casos se les puede proponer que lo echen a suertes con los dados. El juego podría ser el siguiente: uno de ellos elige par o impar, se tiran dos dados, se multiplican los dos números y se mira si el resultado tiene la paridad elegida, si acertó elige la tarea que prefiere sino la elige el otro niño. Podemos preguntar a la clase si conviene elegir par o impar [...] Y ¿qué sucedería si en lugar de multiplicar los resultados de los dos dados los sumáramos? 

Van aprofitar aquest exemple per destacar la importància de les taules de doble entrada per analitzar-los i ara podem afegir un altre exemple en que aquestes taules demostren la seva utilitat: els daus de Sicherman, que apareixen a la imatge següent, tenen la propietat de generar la mateixa probabilitat que dos daus convencionals d'obtenir resultats entre 2 i 12 quan es sumen els dos valors obtinguts en llançar-los (més informació aquí).

Font: http://www.futilitycloset.com/2012/07/25/sicherman-dice/

Volem recordar aquí l'activitat dissenyada per fer en grups a la prova de Competències bàsiques a l'ESO proposada a l'any 2006 (la podeu trobar aquí: el quadern individual i el quadern del grup). Es tracta d'una activitat en que es proposa a cadascun dels integrants del grup tasques específiques per realitzar amb dos daus (han de llançar-los i enregistrar el resultat de la suma, la resta, la multiplicació i el màxim dels dos valors obtinguts) i que al nostre entendre permet explorar molt bé les idees que tenen els nostres alumnes sobre la probabilitat abans de fer servir les taules de doble entrada.

Tres daus i més

En relació a activitats on s'involucra l'ús de tres daus us recomanem aquesta simulació del joc "pedra, paper i tisores" 

https://mathsgear.co.uk/products/non-transitive-grime-dice

Aquests tipus de daus s'anomenen "no transitius" perquè llançant dos d'ells la probabilitat d'obtenir un nombre més gran és major al vermell que al blau, és major al blau que al verd i és major al verd que al vermell. N'hi ha altres ternes de daus amb aquesta propietat, a la propera imatge en trobem un exemple.

Les cares que no es veuen tenen el mateix valor que les oposades visibles
a la imatge. Font: http://es.wikipedia.org/wiki/Dados_no_transitivos

També hi ha quaternes de daus no transitius. Un exemple (coneguts com a daus d'Efron) el trobem en un article del Miguel Barreras al número d'octubre de 2012 de la revista Uno (pàg 53) i també al capítol 28 del llibre del mateix autor "¿Y los ciruelos chinos?" (podeu trobar informació sobre aquest problema aquí ).

http://singingbanana.com/dice/articleold.htm

Per acabar, alguns comentaris més

• a continuació podeu veure un fantàstic vídeo del James Grime on, fins i tot, es pot trobar un joc amb cinc daus d'aquest tipus

 

• De daus no transitus també es parla a Un extraño juego de dados. A més de gràfics molt guapos s'afegeix una altra característica que diferencia el joc amb daus del joc pedra, paper i tissores (la primera diferencia és que amb els daus no hi ha empat). Si tres persones juguen simultàniament ni pedra, ni paper, ni tissora té major probabilitat de guanyar però si tres daus juguen simultaniament hi haurà un que té més probabilitat que els altres de guanyar. 
• Dels 10 esdeveniment possibles en pedra, paper, tissores jugats entre tres persones (r=pedra, p=paper,t=tissores) rrr, ppp, ttt i rpt: generen empats rtt, tpp, prr: hi ha un guanyador, el que tria una cosa diferent trr, ptt, rpp: hi ha un perdedor, el que tria una cosa diferent, però no hi ha guanyador 
• Dels 216 esdeveniments possibles en el llançament dels tres daus utilitzats a http://www.teachmaths-inthinking.co.uk/activities/grime-dice.htm El vermell guanya amb 9xy i 420 (1x6x6+5x3x1=51 del 216 casos possibles) El blau guanya amb 47 y (5x3x6=90 del 216 casos possibles) El verd guanya amb 425 (5x3x5=75 del 216 casos possibles) O sigui que el blau té un 41% de probabilitat de guanyar als altres dos, mentre que la probabilitat del verd és del 35% i del vermell només un 24
• Val la pena l'entrada que sobre aquest tema ha publicat el Joan Jareño al seu blog Calaix

 

• Cut the knot presenta el treball de Bráulio de O. Silveira en relació a l'existència de set conjunts de cinc daus no transitius

http://www.cut-the-knot.org/Probability/Nontransitive-Dice-5.pdf

Encara que no té a veure amb probabilitat, al mmaca ens presenten una altra situació d'ordre "no transitiu"

Materials per treballar la probabilitat: les monedes

Quan els alumnes estudien per primer cop la situació: llenço dues monedes i miro les cares que han quedat cap a dalt, per quina opció apostaries: surten dos nombres, només un nombre o cap? acostumen a pensar que les tres opcions tenen la mateixes possibilitats. Quan experimenten fent alguns llançaments comencen a intuir que l'opció de que surti només un nombre cap a dalt és més freqüent, quan ho fan amb un simulador on poden realitzar moltíssims llançaments comencen a veure que no només és més freqüent sinó que és el doble de freqüent que les altres dues opcions:

En aquesta imatge resultat d'una simulació de 70 llançaments fets amb http://syzygy.virtualave.net/webwork/javascript/23coints.htm es veu que en
35 oportunitats en una de les monedes ha sortit un nombre (un tren aquí) i en
l'altre una cara (de les altres 17 han estat dos cares i 18 dos nombres)

Creiem que per ajudar al alumne a que vegi que en llançar les dues monedes els resultats possibles són quatre i no tres és bo que facin els llançaments amb dues monedes diferents 

Font: http://bilder-bibliothek.blogspot.com.es/  

Amb aquestes monedes, els possibles resultats dels llançaments són: que en les dues quedi el nombre cap a dalt, que en la d'euro quedi el nombre i en la de dolar no, que en la de dolar quedi el nombre i en la d'euro o que no quedi visible cap dels dos nombres. 

Si llanço tres monedes, per quina opció apostaries?

Font: https://commons.wikimedia.org/wiki/File:ThreeCoins.svg 

El simulador utilitzat per a dues monedes també serveix per analitzar aquest experiment

I en aquest altre applet també es pot comparar els llançament de dues i tres monedes: en el cas de dues monedes "en les dues cares surt el mateix" és un esdeveniment de probabilitat un mig però en el cas de tres monedes "en les tres cares surt el mateix" és un esdeveniment de probabilitat un quart. 

En relació al llançament de 4 monedes us proposem l'activitat animada del projecte NRICH The Better Bet: convé apostar perquè surtin exactament dos nombres cap dalt quan llencem 4 monedes? Certament no ja que només tenim 6 possibilitat de guanyar entre 16 resultats possibles. Però si ens proposen que per llançar les monedes es paga 1 euro i cobren 3 euros quan obtenim dues cares, convé jugar-hi?

Ara que ja hem analitzat els llançaments amb 2, 3 i 4 monedes i després de reflexionar sobre el fet de que llançar n monedes és el mateix que llançar una moneda n cops, podem plantejarnos aquest altre problema del NRICH: Thank Your Lucky Stars (penseu que totes les activitats del NRICH porten enllaços cap a la solució del problema, cap a recursos per al professor i cap a problemes semblants)

En relació a l'anàlisi de ratxes en llançar una moneda també hi ha propoestes interessants al NRICH (Last One Standing o What Does Random Look Like? o el vídeo que apareix a la següent imatge)

En el pròxim post dedicat als materials per treballar la probabilitat parlarem de daus i allí comentarem extensament els jocs no transitius, encara que la majoria involucren daus n'hi ha un que involucra el llançament reiterat d'una moneda per la qual cosa pot interessar esmentar-lo en aquest post: El juego de Penney: tirando monedas con curioso resultado.

Per acabar volem parlar d'altres monedes unes de les que hi ha tres tipus: unes que són vermelles pels dos costats, altres que són blaves pels dos costats i altres que són vermelles per un costat i blaves per l'altre. Agafem-ne una de cada tipus, posem-les en una bossa, extraiem una, mirem una de les cares i intentem endevinar el color de la cara que no veiem. Quina és la millor estratègia?

Aquí tenim un simulador d'aquest joc fet pel Joan Jareño

http://www.xtec.es/~jjareno/activitats/atzar/tres_fitxes.htm

I aquí un estudi del problema.

Comentari a posteriori

Durant la X Jornada d'Educació Matemàtica organitzada a l'IEC vam poder escoltar la presentació del grup MatGi "Tema 13: Probabilitat i Estadística" i allí es van proposar materialitzar el problema de Buffon amb monedes. Us recomanem molt els documents que sobre aquest problema trobareu seguint l'enllaç anterio. Destaquem especialment el simulador de l'experiment que ofereixen i la contrastació  de les dades experimentals amb l'anàlisi geomètrica de la posició que han d'ocupar els centres de les monedes perquè no tinguin contacte amb les línies.

Còpia de pantalla obtinguda amb el simulador abans esmentat

Materials per treballar la probabilitat: boles i urnes

Una manera natural de treballar amb fraccions
Imaginem que en una cursa d’obstacles, cada obstacle és una prova que no pots superar fins que no extreguis la bola adequada d'una urna. Però en cada obstacle pots triar si fas la versió A o B de la prova. Si en un cas tens les següents dues versions de la prova, quina triaries?

La relació amb l'ordenació de fraccions i amb el càlcul de probabilitats d'aquesta situació és innegable però podem proposar-la sense haver treballat abans cap dels dos temes de manera explícita a l'aula. Més aviat, podem considerar-la una molt bona situació inicial per introduir qualsevol dels dos temes.

A la Cursa de probabilitat de la Caixa de Varga es poden trobar dotze targetes que combinades entre si donen moltes oportunitats de fer comparacions de fraccions amb el mateix numerador, amb el mateix denominador, etc.

Boles indistingibles

Un problema interessant relacionat amb aquest material és el següent: Si saps que a l’urna hi ha tres boles blanques i una negra i extreus dues, per quina opció apostaries: treure dues boles del mateix color o dues de color diferent?

Aquest problema posa l'atenció sobre la dificultat de comptar bé totes les possibilitats quan tenim elements que no són fàcilment identificables com a diferents. Imaginem que a més de color aquestes boles tenen un nombre diferent cadascuna. Aquí no és difícil identificar l'espai mostral de l'experiment, o el que és el mateix, llistar tots els possibles resultats d'una extracció: 12, 13, 14, 23, 24 i 34. Ara la resposta esdevé senzilla: les dues opcions "treure dues boles del mateix color" o "treure dues boles de color diferent" són igualment probables.

Aquest problema de la distinció entre boles és el mateix que es presenta quan llancem dues monedes i els alumnes pensen que els resultats possibles són 3 quan en realitat són  4 i el mateix que es presenta quan llancem dos daus i els alumnes afirmen que només hi ha una possibilitat de que en sumar els resultats resulti un 11: que en un dau surti un cinc i en l'altre un sis. Aquests dos problemes els discutirem amb més detall en futures entrades del blog dedicades, una a monedes i l'altra a daus.

En aquest sentit, recomanem molt aquest applet del Juan Garcia Moreno:

Esmentat a http://www.didactmaticprimaria.com/2014/06/intuicion-probabilistica.html

També hem tractat aquest problema en la sessió dedicada a Probabilitat del mòdul 2 del curs ARAMAT:

En el primer cas analitzat tenim una bola dels color 1 i tres del color 2, en el segon, dues boles del color 1 i dues del color 2. Hem volgut analitzar amb més profunditat aquestes situacions:

En llegir aquesta taula crida l'atenció que 

• la probabilitat d'extreure boles de colors diferents en el cas en que hi hagi una bola del color 1 i p del color 2 és diferent de la probabilitat d'extreure boles de colors diferents en el cas en que hi hagi dues boles del color 1 i 2p del color 2 (la probabilitat per al cas 1-2 és major que per al cas 2-4) 
• en el cas que d'un color hi hagi dues boles la probabilitat d'extreure boles de colors diferents mai és del 50%

En Contingency in the Mathematics Classroom: Opportunities Taken and Opportunities Missed Tim Rowland justifica que la probabilitat és del 50% en el cas que la quantitat de boles de cada color siguin dos nombres triangulars consecutius (1 i 3, 3 i 6, ....)

Més activitats per fer amb boles i urnes
Amb aquest material també podem fer el problema Quants peixos hi ha en un llac? del que ja vam parlar en aquest blog: com podem estimar el nombre de total de boles que hi ha en una urna molt plena sense haver de comptar-les una a una?

A l'octubre de 2015 El Joan Jareño va publicar un post en el seu blog amb un problema molt senzill i de resposta molt poc intuïtiva que val la pena analitzar: En quin lloc sortitrà?

Traiem boles d'aquesta urna una a una: En quin
lloc pensem que apareixerà la primera bola negra?

Una altra activitat relacionada amb aquest material de la que ja hem parlat en aquest blog és Què hi ha dintre de l'ampolla? i de la qual podem trobar una versió virtual al mòdul ¿El azar es cuestión de suerte? del Màster on-line eMeC elaborat per l'Antoni Gomà i una altra a l'entrada In the bag del projecte NRICH.

I per suposat també podem parlar de la loto 6/49: