Entenem la tomografia com l'obtenció d'una sèrie d'imatges resultants de tallar un cos amb plans equidistants i paral·lels al pla sobre el que es recolza el cos. Per començar en presentem dos exemples: la tomografia d'un prisma de base quadrada i la tomografia d'una piràmide amb la mateixa base i altura.
El següent applet permet visualitzar l'obtenció d'aquestes seccions i també les d'un octaedre regular:
 |
| http://demonstrations.wolfram.com/CrossSectionsOfThreeSolids/ |
Com seria les tomografia d'un prisma de base hexagonal? I d'una piràmide truncada?
En comparar les tomografies d'una semiesfera i d'un con, ens cal una anàlisi una mica més profunda: en els dos casos es tracta de cercles de radi decreixent, però les velocitats d'aquest decreixement són diferents:
En els següents dos vídeos trobareu idees per elaborar les tomografies de dos poliedres regulars obtingudes a partir de l'applet Platonic Solids-Slicing
Com seria la tomografia d'un antiprisma de base hexagonal?
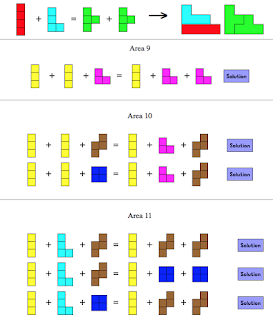
Per acabar podem esmentar les tomografies de cossos formats per cubets, que es converteixen en la seva descripció per capes, una bona manera de il·lustrar situacions com la qua apreixa Visualització amb cubets (II)
 |
| http://demonstrations.wolfram.com/FindTheNumberOfCubesRemoved/ (quan es veu un quadradet negre vol dir que s'ha extret tota la fila de cubets, de dreta a esquerra, de davant a darrera o de dalt a baix) |
Observar que en aquests casos en que hi ha cubets "voladors" aquesta descripció per capes no es pot substituir per una descripció del tipus vista zenital amb informació d'alçades com la que es va analitzar a Quadrats màgics amb retenció de líquids
Es pot practicar amb aquest tipus de descripció amb els següents applets:
- De la col·lecció del Juan Garcia Moreno:
 |
| http://dl.dropboxusercontent.com/u/44162055/manipulables/geometria/codificapoli.swf |
- Del projecte Nrich:
 |
| http://nrich.maths.org/768 |
- Del projecte Wolfram Demostrations
 |
| Laberints tridimensionals la idea és anar del punt vermell al blau considerant que les tres imatges corresponen a tres plantes del laberint (la superior a l'esquerra) |