Dels 880 diferents quadrats màgics diferents de 4x4 aquesta setmana hem sabut a través de Futility Closet que molts retenen líquids.
Què volen dir amb això de retenir líquids?
Pensem en un quadrat màgic com una representació d'alçades d'una construcció feta amb cubets. Aquest tipus de representació la podem treballar amb l'applet Building with blocks que ja havíem presentat en l'entrada Visualització amb cubets però en aquesta ocasió fent servir l'opció Making height numbers.
Diuen que la construcció reté líquids si trobem alguna casella en la que, si "plou", les caselles que té al voltant, per les seves alçades, provocarien embassaments. En el cas de la imatge de l'esquerra (que òbviament no està relacionada amb quadrats màgics) no hi ha cap zona de la construcció on es retenguin líquids però si traduím a una costrucció amb cubets el quadrat màgic de Melancholia I d'Albrecht Dürer podem veure que "reté líquid".
En aquesta última imatge es pot "veure" que la construcció reté líquid a sobre de les torres d'altura 6 i 7
Intentem quantificar el líquid que queda embassat sobre les torres d'altura 6 i 7 (o el que és el mateix, entre les torres d'altura 10, 11, 12, 14, 15 i 9). Si prenem com a unitat de mesura el líquid que cap en una torre d'altura 1, com que l'embassament arribaria fins una altura de 9 (l'altura més baixa de les torres que l'envolten, a la imatge indicada amb groc), a sobre de la torre d'altura 6 es retenen 3 unitats de líquid i a sobre de la torre d'altura 7 se'n retenen 2, donant un total de 5 unitats de líquid embassat.
Això de retenir líquids no és inusual, segons Craig Knecht, 743 dels 880 quadrats màgics de 4x4 en retenen. El màxim que en poden retenir els quadrats màgics de 4x4 són 15 unitats i n'hi ha 12 solucions al problema de trobar els quadrats màgics que retenen aquesta quantitat de líquid:
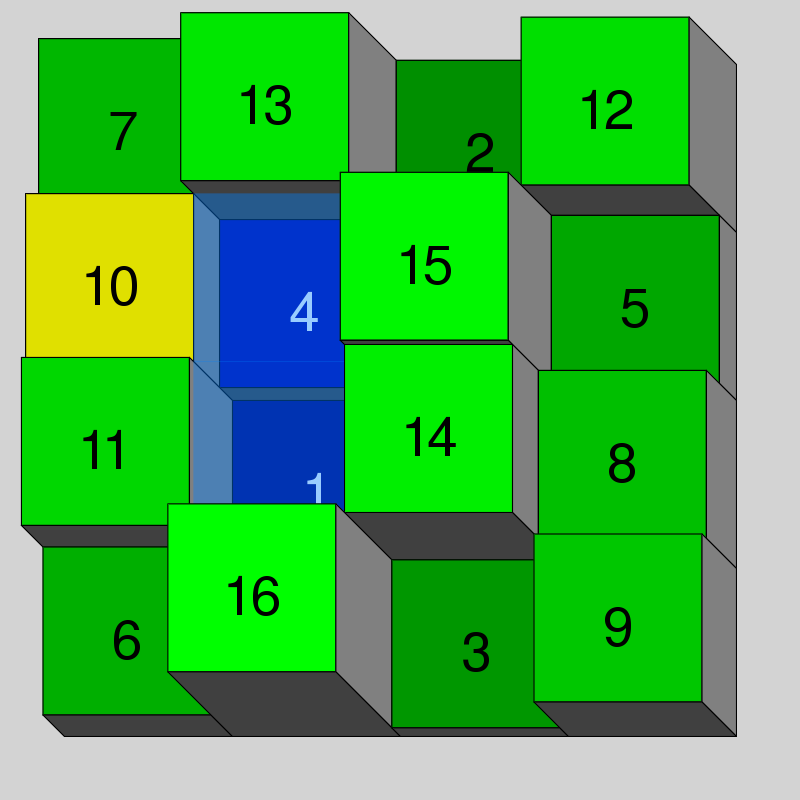 |
| Aquesta és una solució presentada per Hugo Pfoertner en el concurs Magic Water dels Al Zimmermann's Programming Contests |
Aquestes altres dues solucions les hem pogut trobar entre el
llistat de quadrats màgics de 4x4 associatius de la Wikipedia
Però a partir del llistat que apareix a l'informe final del concurs d'Al Zimmermann podem construir les altres 9 solucions.
 |
| Representem una solució fent servir Geogebra (en aquest cas la construcció reté 6 unitats de líquid sobre la torre d'altura 3 i 9 unitats sobre la d'altura 2) |
 |
| Representem una solució fent servir SketchUp (en aquest cas la construcció reté 5 unitats de líquid sobre la torre d'altura 4 i 10 unitats sobre la d'altura 1) |
 |
| I aquí representem les restants set solucions |

.jpg)






Muy original este punto de vista para trabajar el volumen "que no se escapa", la visualización..., me lo apunto para hacerlo en clase.
ResponElimina