Les sumes fins a 20

Ja fa temps, en una trobada molt interessant amb la gent de l'Escola Miquel Martí i Pol de Barberà del Vallès,vàrem parlar del domini necessari de les habilitats bàsiques, en aquest cas concret les descomposicions del 10. Van sortir idees interessants a la conversa, que finalment hem decidit escriure en el present post, ampliant el tema a les sumes fins a 20.

Suma de dígits
Les sumes de dos nombres més petits que 10, són molt interessants des del punt de vista dels inicis del càlcul, ja que es treballen les primeres estratègies. Per comptar quants cubets hi ha en total, si ajuntem dues col·leccions: una de 3 i una de 6 cubets, tres de les estratègies utilitzades per nens petits són:

• comptar-los tots: l'alumne compta 1, 2, 3 i continua 4, 5, 6, 7, 8, 9
• començar pel primer: comença per "encapsular" el tres (el primer sumand) i continua comptant amunt: 4, 5, 6, 7, 8 i 9
• començar pel més gran: sap que 3+6 és el mateix que 6+3, "encapsula" el sis i continua comptant amunt: 7, 8 i 9

També pot passar que algun alumne pensi que 3+6 és el mateix que 5+4 que pot ser un resultat que sàpiga de memòria perquè sap que cinc dits d'una mà i quatre d'altre és el que fa servir per representar el nombre 9 amb els dits. Això ens indica que l'alumne entra en la fase de derivar fets, és a dir "cridar" a un fet conegut per solucionar un fet del que no s'està completament segur.

Organitzar les sumes de dígits:
Seria bo establir un dispositiu de cara al mestre que aprofiti aquestes primeres estratègies emergents i que destaqui el treball de derivar fets de manera organitzada:

• Partint de les estratègies naturals dels alumnes mitjançant el plantejament de situacions "riques" i contextualitzades que promoguin l'ús d'estratègies personals
• Passant de comptar-los tots a començar pel primer
• Introduint l'estratègia començar pel més gran
• Identificant els primers "fets coneguts"(sumes de les que l'alumne pot dir el resultat "de cap")
• Fomentant la deducció de nous fets a partir dels fets coneguts: "fets derivats", establint connexions entre els que ja pot dir "de cap" i el que encara no (fase d'automatització de les sumes de dígits)

Els tres primers punts són força coneguts per tothom, però la mentalitat dels dos últims, en el que recolza la memorització en la deducció és la clau de volta per a un aprenentatge intel·ligent. Cal dir que aquesta estratègia de deduir fets, hi ha força alumnes que l'apliquen de manera natural però aquí estem parlant de explicitar aquesta estratègia, discutir-la amb els alumnes i fomentar-la en l'aula. L'objectiu és que els alumnes passin de calcular comptant a calcular sense comptar.

Un dispositiu com el que ens interessa, que ens dona pistes per organitzar aquests aprenentatges, podria ser el següent:



Sumes +1 i +2
És important que l'alumne identifiqui "sumar 1" amb "dir el següent" i "sumar 2" amb "dir el següent del següent".

Sumes fàcils fins a 10
La part pintada de carbassa correspon a "sumes fàcils fins al 10 amb el gran al davant", un tipus de suma a les que hem de donar molta presència en la nostra aula.
Un cop apreses aquestes sumes, la part lila es pot aprendre deduint fets: 3+7 a partir de 7+3, per exemple.

Sumes dobles i quasi dobles
L'aprenentatge dels dobles (en verd) forma part dels aprenentatges bàsics. Amb aquesta base, els alumnes poden deduir els "quasi dobles" (en lila). En aquest sentit, val la pena veure de nou el vídeo que Carme Barba va gravar amb alumnes de 6 anys, alguns dels quals fan servir aquesta potent estratègia.

Sumes amb resultat 10 i més gran
La part taronja correspon a sumes de resultat 10, un conjunt de sumes per a les quals l'agrupació dels dits de les dues mans són el suport fonamental. La part pintada de lila pot ser resolta per "fets coneguts-fets derivats". 

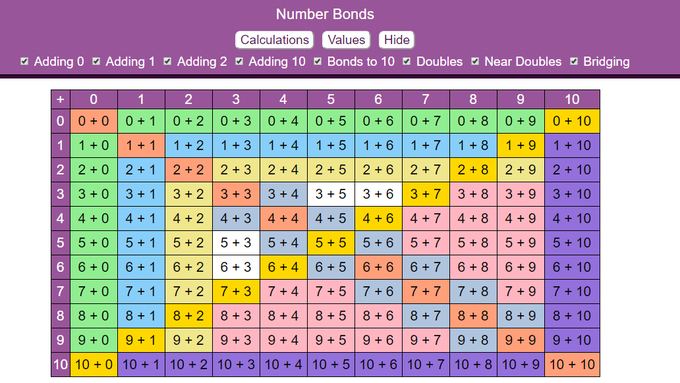Captura d'una graella interactiva que permet treballar
aquestes sumes (via @StudyMaths)

L'estratègia fonamental per a aquestes deduccions és l'anomenada "pas pel 10" que ja havíem esmentat als posts Un material que ensenya i Aritmètica al marge dels algorismes. Per exemple, per sumar 6+8, descomposem el segon sumand en 4+4 (triem aquesta descomposició del 8 perquè a 6 li falten 4 per arribar al 10) i fem 6+4=10 i 10+4=14.

En aquest vídeo de @innovamat_ es veuen alguns exemples d'aplicació d'aquesta estratègia contextualitzats amb oueres de 10

Una estratègia que es pot practicar així:

"Laboratori de nombres" (1r Primària, Innovamat)

Amb targetes que recreen les oueres i fitxes

Com haureu observat, per a moltes de les sumes hi ha més d'una estratègia per fer-la. És molt possible que en arribar a les sumes entre 10 i 20 certs alumnes les sàpiguen fer, sense ajuda, però n'hi haurà que no, i això els portarà a aplicar de nou estratègies conegudes (posar el gran al davant) però no assolides.

Referències:

• Torbeyns, J., Verschaffel, L., Ghesquière, P. (2002). Strategic competence: Applying Siegler’s theoretical and methodological framework to the domain of simple addition. European Journal of Psychology of Education, 17(3), 275.
• Van den Heuvel-Panhuizen, M., TAL Team. (2008). Children learn mathematics: A learning-teaching trajectory with intermediate attainment targets for calculation with whole numbers in primary school. Sense Publishers.

Estratègies alternatives

Aquest "camí d'assoliment d'estratègies de càlcul" ens pot ajudar molt a crear una bona base pel càlcul, però paral·lelament hi ha un altre punt important, i segurament el més matemàtic de tots: la utilització d'estratègies alternatives o personals. Un exemple seria que per sumar 7+9, un alumne sumés 10 i restés un..."perquè li és més fàcil" Aquests descobriments matemàtics s'han de celebrar! ... sempre que siguin eficaços.

Un altre exemple el tenim en l'estratègia que fa servir l'última nena del vídeo de la Carme Barba esmentat a dalt. Fixeu-vos que en aquest cas la nena ha utilitzat una "estratègia de compensació" buscant un fet conegut (4+3) traient una unitat del primer nombre per a afegir-li al segon.

La pràctica d'aquestes sumes

De vegades entendre la suma solament com a operació a resoldre i no anar més enllà ens tanca maneres de mirar. Podem pensar que la suma és una relació que aglutina els nombres de tres en tres. Així per exemple, el 10 el 3 i el 7 sempre van junts. Aquesta idea es pot representar en un triangle, en el que tapant un dels tres nombres cal trobar el que falta.

Informació al post:Triangles aritmètics 1 (descomposició de dígits)

Aquesta encapsulació de tres nombres en una terna també presenta idees interessants de cara al treball amb les restes ja que es dona el cas que alumnes que dominin perfectament i amb rapidesa el triangle (14,8,6), sabran que 14-8=6 i 14-6= 8.

Hem de tenir en compte que en practicar aquestes sumes i fomentar l'encapsulació, no es tracta d'anar proposant moltíssimes sumes fins que les aprenguin de memòria sinó de generar un treball on cada alumne es vagi plantejant preguntes com aquestes:

• Quines són les sumes que em sé?
• Quines les que tinc dubtes? Com puc fer per aprendre-les? Amb quina suma que ja sé puc relacionar-la?

No podem limitar l'adquisició d'aquests automatismes a sessions específiques de càlcul. Cal aprofitar altres activitats, que facin pràctica en un ambient de resolució de problemes. Per exemple, la que vam relatar en el post Construir cases

Tornem al començament
La conversa amb les mestres va ser interessant i desafiant, va plantejar preguntes importants.

• En una escola que es treballa per projectes, com es pot treballar l'adquisició d'aquestes habilitats?
• Hi caben tasques amb un objectiu específic com l'aprenetatge de calcular sense comptar, que es desenvolupin en paral·lel, fins i tot, anant més enllà en el temps que la finalització del projecte?
• Metodològicament, com s'haurien de plantejar aquestes tasques de manera que l'ambient de classe no sigui "diferent" quan fem treball específic matemàtiques? Com podem fer perquè la pràctica d'aquestes habilitats bàsiques no es visqui com a una proposta de tasques per memoritzar sumes? És possible? Des del Puntmat pensem que si, però necessitem discutir-ho amb vosaltres.