La setmana vinent vull fer una activitat lligada a la vida quotidiana i les antenes estan a punt per a localitzar Matemàtiques mentre vaig pel carrer. Entro a buscar diners a un caixer per pagar al lampista (ell m'ha dit que em costaria prop de 300 €). Penso que si en trec 300, el caixer em pot donar 6 bitllets de 50 i per tant, per poder tenir més possibilitats de pagar l'import exacte, trio demanar 280 €.
Mentre espero em plantejo la pregunta que ràpidament decideixo que portaré a classe la setmana vinent.
Quines quantitats puc obtenir en un caixer automàtic que solament et dóna bitllets de 50 i de 20?
Evidentment la primera conclusió és que han de ser múltiples de 10, però quins d'aquests múltiples puc obtenir? Pensant ja en l'activitat van sorgir les primeres preguntes a formular:- De quantes maneres diferents pots pagar 170€ utilitzant bitllets de 20 i de 50?
- Quina de les quantitats següents puc treure i queines no (30, 130, 270...)
- Suposant que el caixer et dóna sempre la menor quantitat de bitllets (per exemple, en el cas del 280: 4x50+4x20) i pressuposant que el meu lampista no porta mai canvi. Quins preus podré pagar justos?
-
- En el cas de treure 280 podria pagar just: 20, 40, 50, 60, 70, 80, 90, 100... i no podria pagar 10, 30, 210, 230, 250, 270 i òbviament preus més grans que 280
- Però si demanem 290 (5x50+2x20) el que puc pagar és 20, 40, 50, 70, 90, 100, 120, 140, 150, 170... però no podria pagar 30, 60, 80, 160, 180, 260, 280
Investiguem ara la pregunta inicial:
- Quines quantitats puc treure, i quines no, utilitzant únicament bitllets de 20 i de 50?
Si com a pista per a solucionar el problema suggerim als alumnes que vagin anotant els resultats en una graella com la de sota, els serà més fàcil trobar la solució. Per exemple quan ja sabem que es poden obtenir 70€ (50+20) totes les quantitats de la seva columna també es pot obtenir ja que van de 100 en 100
10 20 30 40 50 60 70 80 90 100
110 120 130 140 150 160 170 180 190 200
etc.
Construir un algorisme
Quina creiem que és la lògica interna del caixer? Comença pagant amb un mínim de bitllets fins que s'acaben les existències d'un dels dos tipus? Si suposem que si, podem plantejar que escriguin les instruccions que calguin perquè un robot (un company o el mateix professor/a) sàpiga quants bitllets de cada tipus ha d'agafar per donar el mínim de bitllets quan li demanen una quantitat determinada.
Segurament els nostres alumnes començaran per observar regularitats a partir de les descomposicions
- 100 =2x50
- 110 = 1x50 + 3x20
- 120 = 2x50+ 1x20
- 130 = 1x50 + 4x20
- etc
Més aviat o més tard podran arribar a formular cert algorisme fixant-se amb la paritat o no de la xifra de les desenes.
Finalment i ja de tornada a casa a pagar al lampista, una última idea: quina hauria de ser la proporció de bitllets de 20 i 50 que ha de posar l'encarregat d'omplir de bitllets el caixer?
Ampliació
 |
| Clicar per ampliar imatge. Llibre Fisher, Vince |
Aquesta activitat és "filla" de la plantejada al magnífic llibret d'activitats "Investigando las Matemáticas. Libro 2 fet per R. Fisher i A. Vince (original del 1988 i traducció del 1990). La col·lecció consta de quatre llibrets, i està descatalogada.
Si tinc segells de 5 i de 7, quins valors puc obtenir?
A la guia pel professorat indica una fórmula general per trobar-lo, encara que restringida a parelles de nombres que tinguin MCD 1. Siguin a i b els nombres, per trobar el nombre inicials a partir del qual ja es poden obtenir tots els nombres cal fer: (a-1)·(b-1). (en al cas del problema dels segells el número seria el 24)
Anant més enllà del llibre i pujant força el nivell: què passaria en cas que el mcd no fos 1? quina seria la fórmula?
Com veieu, aquest és un problema amb gran potencialitat ja que depenent de les preguntes o dels nombres d'entrada, es pot treballar a edats molt diferents.
Altres formulacions del mateix problema
- A la web del Calaix +ie el Joan Jareño ens proposa un magnífic joc de càlcul, el TOC BUM, que té la mateixa base matemàtica.
 |
| Captura de pantalla |
- El matemàtic J.H. Conway va idear un altre joc relacionat amb el problema al voltant del qual gira aquesta entrada. Es poden trobar les seves regles i un applet per jugar a Sylver Conaige
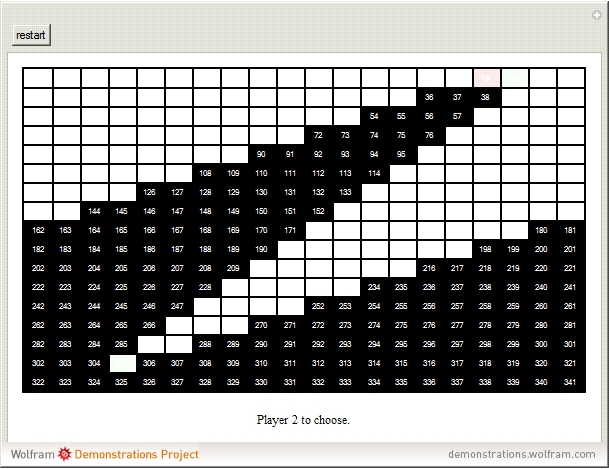 |
| Captura de pantalla |
- Els "locos lindos" de Numberphile es pregunten com es poden comprar exactament 43 McNuggets de pollastre atenent a que els venen en caixes de 6, 9 i 20 peces

M'ha agradat molt aquesta entrada ja que molts cops m'he preguntat per què no donen bitllets de 10 € als caixers. Em sembla una activitat molt interessant i molt lligat a l'ús de les matemàtiques en el nostre dia a dia. Gràcies
ResponElimina