PuntMat: Perímetre i àrea 3

Després de les activitats suggerides als posts Perímetre i àrea 1 i Perímetre i àrea 2, en aquest post proposem unes noves activitats que pretenen oferir experiències als alumnes perquè interioritzin el fet no trivial de que aquestes dues magnituds es poden modificar de manera independent.

Primera activitat: pensament exhaustiu

A la graella que apareix a l'esquerra cada quadre mesura 1cm de costat. Pinta alguns dels seus quadres de manera que quedi una figura (única i sense forats) de 12 cm de perímetre. Quantes solucions realment diferents pots trobar?

A la imatge es poden veure les 16 solucions trobades per un alumne de 5è de primària:

Si en lloc de mantenir constant el perímetre, demanem les figures que es poden fer sobre la mateixa graella de 6 cm² d’àrea, les solucions són vuit (una de perímetre 10 cm, una altra de perímetre 11 cm, una altra de perímetre 14 cm i cinc de perímetre 12 cm):

En la següent imatge ja es pot intuir una propietat de les figures formades per la unió de quadrets que consisteix en que si el quadret que s'elimina està a la "cantonada" el perímetre no s'altera.

Feina encara sense acabar d'un alumne cercant les figures de perímetre 12 cm

Volem aprofundir en aquesta "propietat" a la segona activitat.

Comentari a posteriori
Si l'activitat anterior la proposem sobre paper quadriculat sense restringirse a una graella de 3x3 el nombre de solucions varia de manera considerable

les solucions de perímetre 12 cm passen de 16 a 25

les solucions d'ârea 6 cm² de 8 a 35

Aquestes 35 figures d'àrea 6 es coneixem com a hexaminos

Segona activitat: cerca de patrons i regularitats

En aquestes graelles també cada quadre mesura 1cm de costat.

Transforma la figura vermella en una altra canviant únicament un dels seus quadrets de lloc, de manera que la figura no es trenqui.

Verifica que es poden obtenir 12 noves figures però que cap d'elles té el mateix perímetre que la vermella (cinc d'elles tenen perímetre 14 cm i les altres set, perímetre 12 cm; els perímetres més grans els obtenim quan el quadret que movem és el que no està a les cantonades del rectangle vermell).

Transforma la figura verda en una altra canviant únicament un dels seus quadrets de lloc, de manera que la figura no es trenqui i el perímetre de la nova figura sigui major.

Pots canviar qualsevol dels quadrets? A quines noves posicions els pots moure?

Es pot fer el mateix amb l'objectiu de que el perímetre de la nova sigui menor que el perímetre de la figura inicial?

La @OhYahLee proposa una tasca similar amb material manipulatiu: es poden afegir tres rajoles sense alterar el perímetre de la figura resultant?

I afegint les tres rajoles alhora permet donar una resposta afirmativa a la pregunta plantejada.

Val la pena destacar que aquests patrons que pretenem que els alumnes descobreixin estan involucrats en la següent pregunta de les proves PISA en que es demana als alumnes que triïn quins dissenys són vàlids per al fuster:

Podeu accedir al document complet clicant aquí

Tercera activitat
Una manera de posar en pràctica aquest patorns descoberts és omplir la taula de la imatge de manera que en una mateixa fila les figures comparteixen àrea però el perímetre augmenta i en una mateixa columna les figures comparteixen perímetre però l'àrea augmenta:

La taula buida

Un exemple de taula plena

Podeu veure alguns suggeriments de com portar aquesta activitat a l'aula en aquest vídeo gravat durant una de les sessions del curs ARAMAT dedicada a mesura i transformacions

També podeu veure com van portar l'activitat a l'aula de 1r d'ESO els amics de l'INS Baixamar en aquesta entrada del seu blog:

Quarta activitat:
Pinta 27 quadrets d'un full quadriculat de manera d'obtenir una figura de perímetre mínim. Ja sabem que entre els dos rectangles que es poden fer pintant 27 quadrets el de 9x3 té menor perímetre (24) però ens interessa saber de l'existència d'una figura de menor perímetre.

A la imatge es veu una d'aquestes figures:

Si volem extendre aquesta tasca a altres quantitats de quadrets ens trobem que no sempre es pot aconseguir una figura amb menys perímetre que el rectangle òptim (el que s'assembli més a un quadrat) i pot sorprendre comprovar que això no només és impossible amb quantitats que siguin quadrats perfectes:

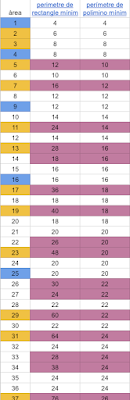taula

La taula anterior feta a partir de A262767 i A027709 mostra un patró molt interessant en relació al perímetre mínim quan varia el nombre de quadrets pintats (un 4 i un 6, dos 8 i dos 10, tres 12 i tres 12, ...) i malgrat que els alumnes no tinguin una fórmula explícita per repondre, és interessant pereguntar-los, per exemple, quin serà el perímetre mínim d'una figura que ocupi 70 quadrets.

Cinquena tasca:
Entre les solucions de perímetre 12 de la primera activitat, 5 és la menor àrea aconseguida, però sabem que amb perímetre 12 es poden aconseguir polígons d'àrea tan petita com es vulgui (per exemple, partint d'un paral·lelogram de costat 1 i 5 es pot anar fent l'altura més i més petita). El problema aquí és calcular el valor de l'àrea sense conèixer la mida de l'altura.

Martin Garner en "My Best Mathematical and Logic Puzzles", sota el nom "The 12 Matches" va proposar el repte de trobar figures d'àrea 4 amb 12 escuradents i Alex Bogomolny en "Cut the Knot" va extendre la pregunta a àrees 3 i 2.

Tal com es veu a la imatge anterior solucions per a àrea 4 i 3 es poden aconseguir a partir de modificar rectangles però aquesta no és l'estratègia principal que suggereixen ni Gardner ni Bogomolny, sinó que ho fan a partir del triangle rectangle de costats 3, 4 i 5 i àrea 6.