Els primers nombres quadrats (II)

Seguint la proposta del post Els primers nombres quadrats (I) aquí continuarem comentant alguns exemples d'activitats que al nostre entendre permeten als alumnes familiaritzar-se amb els primers nombres quadrats en un ambient de resolució de problemes.

1) Quadrat més proper
Quin és el nombre quadrat més proper als següents nombres? 

• 1x2x3x4 
• 2x3x4x5
• 3x4x5x6 
• 4x5x6x7 
• ...

Font: Product of four consecutive integers
Solució: Si els alumnes coneixen els primers nombres quadrats podran observar que els resultats d'aquestes multiplicacions són sempre el nombre anterior a un nombre quadrat i alguns podran anar més enllà: el resultat de a·b·c·d és el nombre anterior al quadrat de a·d+1 o c·d-1

2) Quadrats consecutius
Escriu, en ordre, quatre nombres quadrats consecutius. Suma els dos dels extrems. Suma els dos del mig. Què hi observes?

Solució: La suma dels extrems és sempre 4 unitats major que la suma del mitjos. Aquesta regularitat a l'igual que l'anterior són fàcilment justificables algebraicament però no és aquest l'objectiu principal de l'activitat, que recordem que és familiaritzar-se amb els nombres naturals i establir conjectures en relació als patrons que hi puguin detectar.

3) La xifra final dels nombres quadrats
Escriu els primers nombres quadrats en ordre creixent i analitza la xifra de les unitats de cadascun d'ells. Què observes?

Solució: A partir d'aquests primers casos els alumnes poden conjecturar que cap nombre quadrat acaba en 2, 3, 7 o 8 o poden detectar que la xifra de les unitats segueix un cicle: 1, 4, 9, 6, 5, 6, 9, 4, 1, 0 i torna a començar. Aquest cicle no es trenca degut a la propietat que exposa el següent diagrama en relació a què passa en elevar un nombre al quadrat: si acaba en 0, 1, 5 o 6 el resultat acaba en la mateixa xifra, si acaba en 2 o 8 el resultat acaba en 4, si acaba en 3 o 7 el resultat acaba en 9, si acaba en 4 el resultat acaba en 6 i si acaba en 9 el resultat acaba en 1. 

Ampliació: Quines poden ser les dues últimes xifres d'un nombre quadrat?

Solució: Mentre que l'última xifra dels nombres quadrats poden ser 6 valors entre els 10 possibles, les últimes dues xifres poden ser 22 entre les 100 possibles (apareixen ressaltades en la següent tabla):

4) La xifra inicial dels nombres quadrats
Quin és el primer nombre quadrat que comença en 5?

Solució: El primer nombre és 529 (el quadrat de 23) però no és el dígit que més triga en aparèixer a la xifra inicial dels nombres quadrats (el 7 no apareix fins al quadrat de 27, 729). Val a destacar que les primeres xifres dels nombres quadrats no segueixen un patró com els que hem observat en les últimes xifres.  

5) Collar de perles quadrades
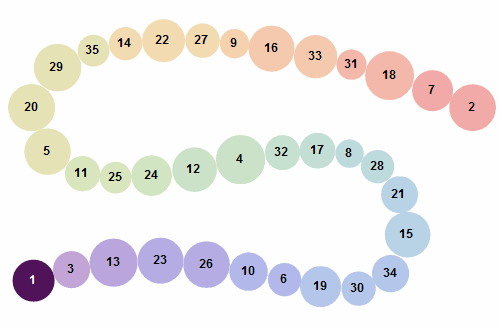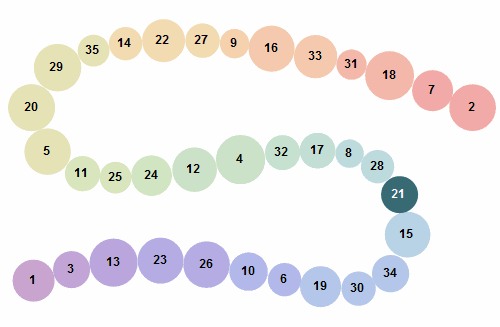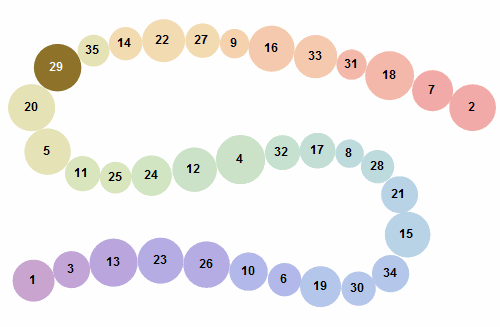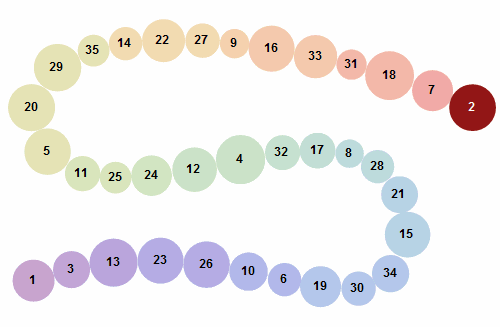
Reordena els nombres de l'1 al 35 perquè la suma de dos nombres adjacents sigui un nombre quadrat

Solució: 

enllaç

A la imatge anterior es veu un collar obert i al rang 1-35 però aquí es pot trobar una distribució que permet fer un collar tancat en aquest rang (1 35 29 20 16 33 31 18 7 9 27 22 14 2 23 26 10 6 19 30 34 15 21 28 8 17 32 4 5 11 25 24 12 13 3) i també en rangs més grans (fins i tot 1-50)