Però a més de saber identificar els nombres quadrats creiem en la importància de que els alumnes memoritzin alguns d'ells per poder avançar en tasques posteriors sense haver d'aturar-se a verificar si són quadrats o no. A més creiem que aquesta memorització pot desenvolupar-se en un ambient de resolució de problemes.
En aquest post, a l'igual que vam fer a Els primers nombres primers, volem comentar alguns exemples d'activitats que al nostre entendre permeten als alumnes familiaritzar-se amb els primers nombres quadrats i que poden resoldre simplement coneixent els 20 nombres quadrats més petits que 400.
1) Suma de quatre quadrats
Solució: Les nou descomposicions del 90 són 9+81, 1+25+64, 16+25+49, 1+4+4+81, 1+4+36+49, 1+9+16+64, 4+25+25+36, 9+9+36+36 i 9+16+16+49. Podem proposar als alumnes que trobin aquestes descomposicions de manera cooperativa i, als alumnes que presentin més dificultats amb la tasca, els podem donar 90 cubets encaixables i demanar-los que els agrupin en 4 o menys quadrats. També es pot simplificar la tasca canviant el 90 per un 50 que té cinc descomposicions possibles.
Els dos nombres entre 50 i 100 que admeten una única descomposició són 56=4+16+36 i 96=16+16+64 (novament creiem que es tracta d'una tasca adient per ser resolta de manera cooperativa, donem a cada alumne dos nombres entre 50 i 100 i els demanem que els descomponguin, en el moment que surtin dues possibilitats, de dos alumnes diferents, descartem el nombre com a resposta a la pregunta formulada).
A @escolasadako les mestres de 6è van proposar als seus alumnes experimentar amb el teorema en un altre format igualment productiu:
2) Restant el major quadrat
Restant sempre el major quadrat possible arribem des de qualsevol nombre al 0. Però quantes restes necessitem? El 96 requereix cinc restes: 96 → 96-81=15 → 15-9=6 → 6-4=2 → 2-1=1 → 1-1=0
Font: Hem conegut aquesta formulació del problema a través de @willhek1
Solució: 23 és el menor nombre que requereix 5 restes: 23 → 7 → 3 → 2 → 1 → 0 i 167 el menor nombre que requereix 6 restes: 167 → 23 → 7 → 3 → 2 → 1→ 0.
Més resultats a A006892 i A053610
3) Suma de dos quadrats
A) Quins nombres menors que 100 es poden escriure com a suma de dos quadrats?
Solució: Observa la imatge que hi ha a a continuació: a la taula de l'esquerra es poden veure els 43 nombres menors que 100 que poden ser descomposts com a suma de dos quadrats.
A partir d'una taula com aquesta taula els alumnes poden conjecturar que cap nombre anterior a un múltiple de 4 es pot escriure com a suma de dos quadrats. Els alumnes més grans, poden investigar les descomposicions factorials dels altres nombres que no es poden descompondre com a suma de dos quadrats (mirar la taula de la dreta) i i poden fer altres conjectures que s'apropin al teorema dels dos quadrats de Fermat (també conegut com a teorema de Nadal atenent a que es diu que el va demostrar el 25 de desembre de 1640) que afirma que
Solució: Per exemple, si els alumnes han triat 16 i 25 que sumen 41, ara han de buscar dos quadrats que sumin 82 (1+81). Trobar aquesta segona parella sempre és possible.
La justificació visual d'aquest fet es pot veure a la següent imatge: el quadrat vermell i el quadrat blau representen la primera parella triada i el doble d'aquesta suma està representat en la part superior de la imatge, a la part inferior de la imatge es veu com les peces es poden reorganitzar (retallant el rectangle groc de la dreta i posant-lo en el lloc marcat en groc fosc) com si fossin peces d'un puzle per obtenir una parella de quadrats que apareixen en gris (els destinataris d'aquesta justificació són els mestres i els alumnes més inquiets però de cap manera la seva presentació és la fita de l'activitat, la qual continua sent la familiarització amb els nombres quadrats):
Encara més, en la imatge hi ha amagada una estratègia per resoldre la tasca: si els primers quadrats triats són a2 i b2, els que s'han de trobar poden ser (a+b)2 i (a-b)2.
L'activitat aquí proposada és un cas particular d'aquesta altra: "Tria dos nombres quadrats i suma’ls. Tria altres dos nombres quadrats i suma'ls (poden ser els mateixos que abans). Multiplica els dos resultats anteriors i troba dos quadrats que sumin el resultat de la multiplicació".
4) Diferència de dos quadrats
Quins nombres es poden expressar com a diferència de dos nombres quadrats?
Solució: Si proposem la tasca de manera cooperativa (cada grupet d'alumnes s'encarrega d'analitzar una desena de nombres) i demanem als alumnes que vagin acolorint els resultats obtinguts en una graella del 100 que posem a la pissarra, es pot conjecturar que els nombres que es poden expressar restant dos nombres quadrats són tots els senars i dels parells la meitat (graella de l'esquerra a la següent imatge).
Si la graella que posem a la pissarra és una graella multiplicativa es pot conjecturar que els nombres que es poden expressar restant dos nombres quadrats són els resultats de parell x parell, senar x senar o múltiples de 4 per qualsevol nombre (graella de la dreta a la següent imatge).
5) Divisions de nombres quadrats I
Tria un nombre i suma-li 3, divideix el quadrat del nombre triat entre el resultat de la suma. Fes-ho amb diferents nombres de sortida, què hi observes?
Solució: Encara que en un inici no sembla que hi hagi cap patró a partir de la setena divisió aquest patró es fa evident
Per suposat que la validesa de la conjectura sobre la invariabilitat del residu i la relació entre el nombre triat i el quocient es pot justificar algebraicament (n2=(n+3)(n-3)+9) però segurament els alumnes als que hem proposat la tasca encara no han treballat amb tanta àlgebra com per ser convençuts per aquesta igualtat. Per tant, creiem més oportú presentar-los una justificació visual: en dividir un quadrat de costat n en grups de n-3 elements, resultat n+3 grups i ens sobren 9 quadrets.
Variants del problema: si proposem als alumnes triar un nombre i sumar-li 1 en lloc de sumar-li 3, el patró en els residus i els quocients es fa evident des de la primera divisió. També es pot sumar 2 o qualsevol altre nombre: el residu a partir d'una certa divisió sempre serà el nombre sumat al quadrat.
6) Divisions de nombres quadrats II
Divideix els primers nombres quadrats entre 4, què hi observes?
Solució:
Els alumnes que trien fer divisions decimals veuen que per als quadrats parells el quocient és un nombre enter i per als quadrats senars el quocient sempre té la forma x,25. Els alumnes que trien fer divisions enteres veuen que per als quadrats parells el residu sempre és 0 i per als quadrats senars el residu sempre és 1. El que té més gràcia és quan s'adonen que els quocients compleixen un interessant patró de creixement tal com es veu a la imatge (recull de resultats de les divisions de 1:4 a 100:4 fetes per un alumnes de 1r d'ESO)1) Suma de quatre quadrats
El matemàtic Joseph Louis Lagrange en 1770 va demostrar que “Tots els nombres enters es poden descompondre com a suma d'un màxim de quatre nombres quadrats”.
Tal com es veu en l'animació anterior aquesta descomposició no és única
a) 90 és el nombre de dues xifres que admet més descomposicions diferents: quantes en té?
b) quins són els dos únics nombres entre 50 i 100 que admeten una única descomposició?
Els dos nombres entre 50 i 100 que admeten una única descomposició són 56=4+16+36 i 96=16+16+64 (novament creiem que es tracta d'una tasca adient per ser resolta de manera cooperativa, donem a cada alumne dos nombres entre 50 i 100 i els demanem que els descomponguin, en el moment que surtin dues possibilitats, de dos alumnes diferents, descartem el nombre com a resposta a la pregunta formulada).
A @escolasadako les mestres de 6è van proposar als seus alumnes experimentar amb el teorema en un altre format igualment productiu:
2) Restant el major quadrat
Restant sempre el major quadrat possible arribem des de qualsevol nombre al 0. Però quantes restes necessitem? El 96 requereix cinc restes: 96 → 96-81=15 → 15-9=6 → 6-4=2 → 2-1=1 → 1-1=0
- quin és el menor nombre que requereix cinc restes?
- quin és el menor nombre que requereix sis restes?
Font: Hem conegut aquesta formulació del problema a través de @willhek1
Solució: 23 és el menor nombre que requereix 5 restes: 23 → 7 → 3 → 2 → 1 → 0 i 167 el menor nombre que requereix 6 restes: 167 → 23 → 7 → 3 → 2 → 1→ 0.
Més resultats a A006892 i A053610
3) Suma de dos quadrats
A) Quins nombres menors que 100 es poden escriure com a suma de dos quadrats?
A partir d'una taula com aquesta taula els alumnes poden conjecturar que cap nombre anterior a un múltiple de 4 es pot escriure com a suma de dos quadrats. Els alumnes més grans, poden investigar les descomposicions factorials dels altres nombres que no es poden descompondre com a suma de dos quadrats (mirar la taula de la dreta) i i poden fer altres conjectures que s'apropin al teorema dels dos quadrats de Fermat (també conegut com a teorema de Nadal atenent a que es diu que el va demostrar el 25 de desembre de 1640) que afirma que
- un nombre és suma de dos quadrats si i només si cadascun dels seus factors primers de la forma 4 k + 3 intervé amb una potència parell.
- un nombre primer es pot escriure de manera única com a suma de dos quadrats si i només si és de la forma 4n+1. Ho ilustrem amb una altra animació de @funfunfunctions
B) Tria dos nombres quadrats i suma’ls. Troba dos quadrats que sumin el doble que els primers.
Solució: Per exemple, si els alumnes han triat 16 i 25 que sumen 41, ara han de buscar dos quadrats que sumin 82 (1+81). Trobar aquesta segona parella sempre és possible.
La justificació visual d'aquest fet es pot veure a la següent imatge: el quadrat vermell i el quadrat blau representen la primera parella triada i el doble d'aquesta suma està representat en la part superior de la imatge, a la part inferior de la imatge es veu com les peces es poden reorganitzar (retallant el rectangle groc de la dreta i posant-lo en el lloc marcat en groc fosc) com si fossin peces d'un puzle per obtenir una parella de quadrats que apareixen en gris (els destinataris d'aquesta justificació són els mestres i els alumnes més inquiets però de cap manera la seva presentació és la fita de l'activitat, la qual continua sent la familiarització amb els nombres quadrats):
L'activitat aquí proposada és un cas particular d'aquesta altra: "Tria dos nombres quadrats i suma’ls. Tria altres dos nombres quadrats i suma'ls (poden ser els mateixos que abans). Multiplica els dos resultats anteriors i troba dos quadrats que sumin el resultat de la multiplicació".
4) Diferència de dos quadrats
Quins nombres es poden expressar com a diferència de dos nombres quadrats?
Solució: Si proposem la tasca de manera cooperativa (cada grupet d'alumnes s'encarrega d'analitzar una desena de nombres) i demanem als alumnes que vagin acolorint els resultats obtinguts en una graella del 100 que posem a la pissarra, es pot conjecturar que els nombres que es poden expressar restant dos nombres quadrats són tots els senars i dels parells la meitat (graella de l'esquerra a la següent imatge).
Si la graella que posem a la pissarra és una graella multiplicativa es pot conjecturar que els nombres que es poden expressar restant dos nombres quadrats són els resultats de parell x parell, senar x senar o múltiples de 4 per qualsevol nombre (graella de la dreta a la següent imatge).
 |
| En lila apareixen els nombres 1 i 4 perquè necessiten del 0 per poder obtenir-los com a diferència de nombres quadrats |
Tria un nombre i suma-li 3, divideix el quadrat del nombre triat entre el resultat de la suma. Fes-ho amb diferents nombres de sortida, què hi observes?
Solució: Encara que en un inici no sembla que hi hagi cap patró a partir de la setena divisió aquest patró es fa evident
6) Divisions de nombres quadrats II
Divideix els primers nombres quadrats entre 4, què hi observes?
Solució:
En la següent imatge es veu una justificació visual d'aquest comportament:
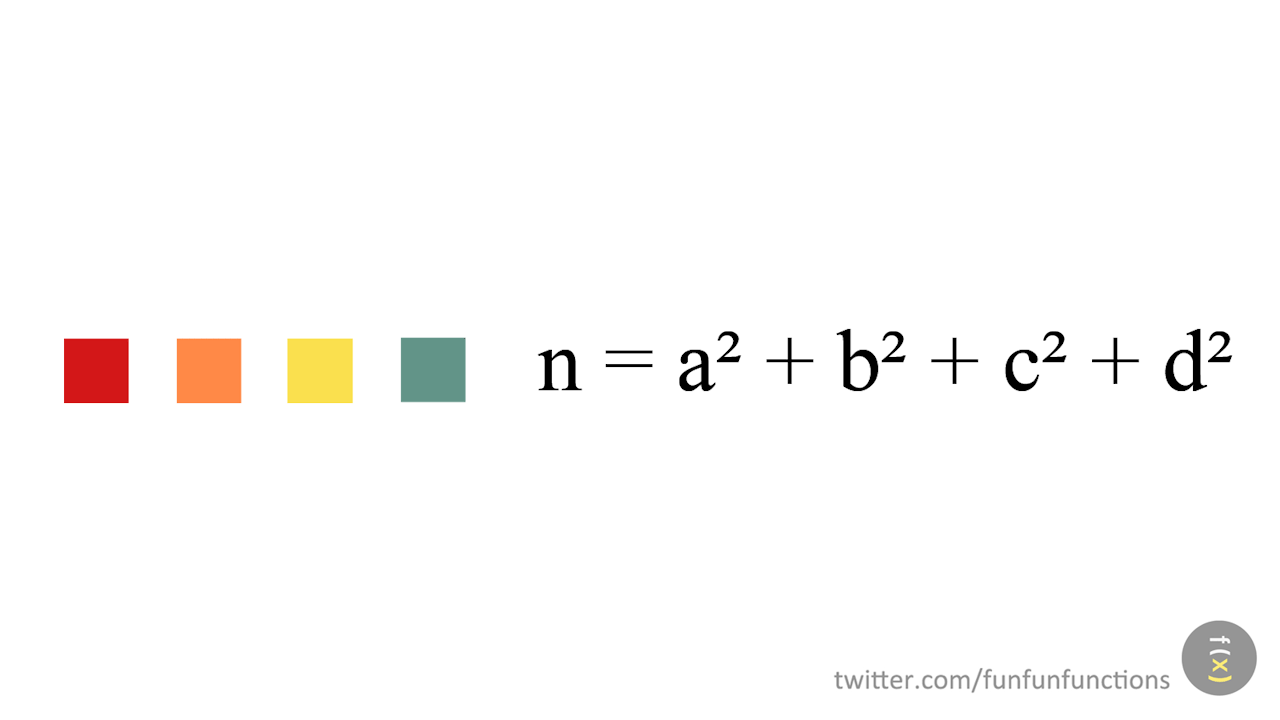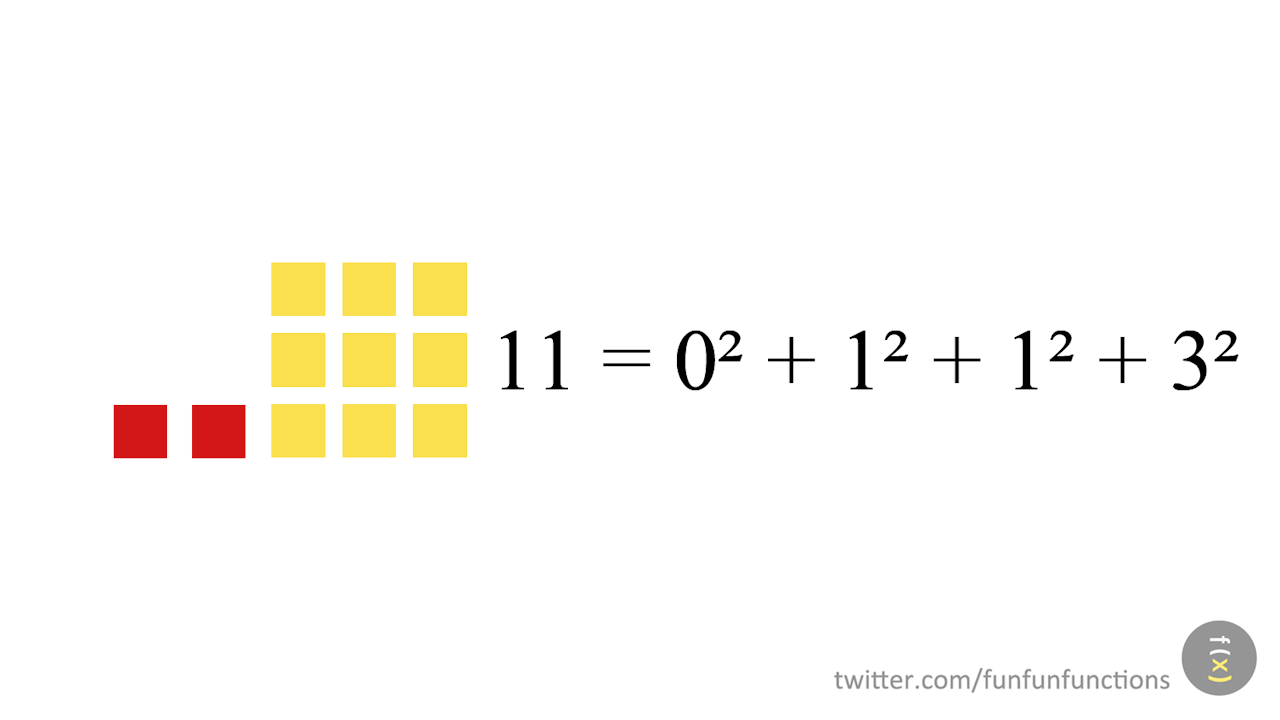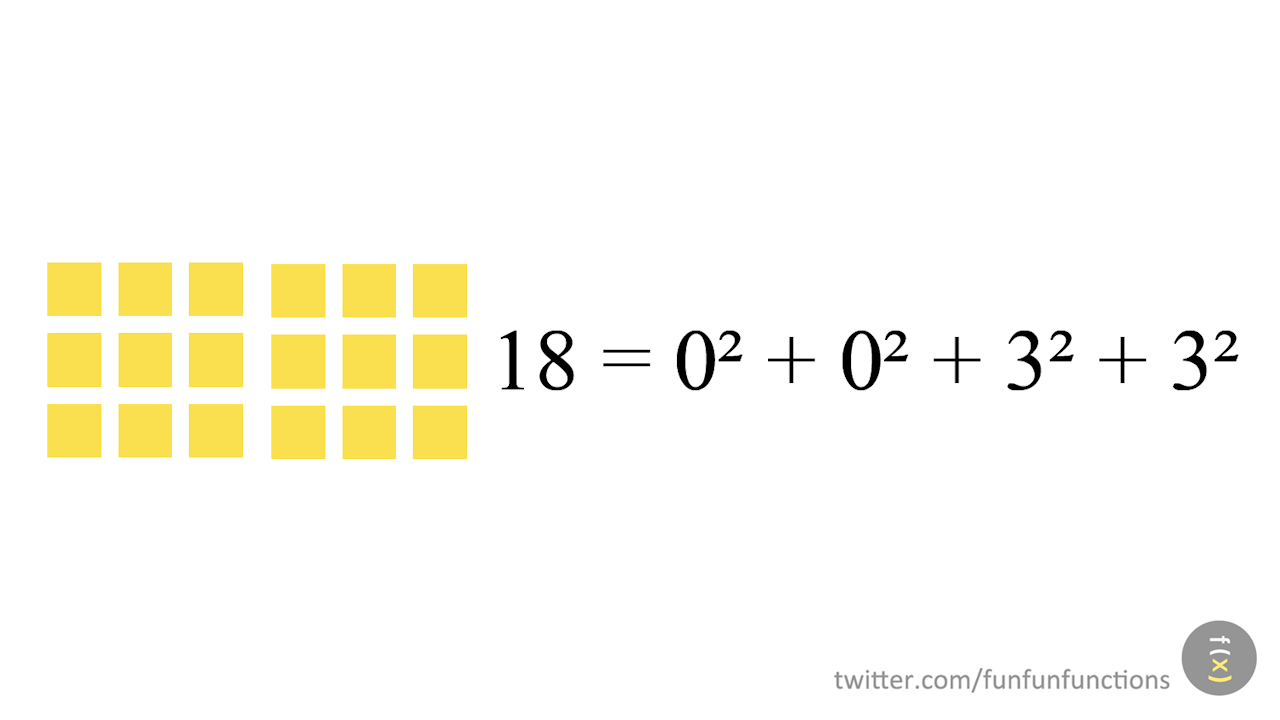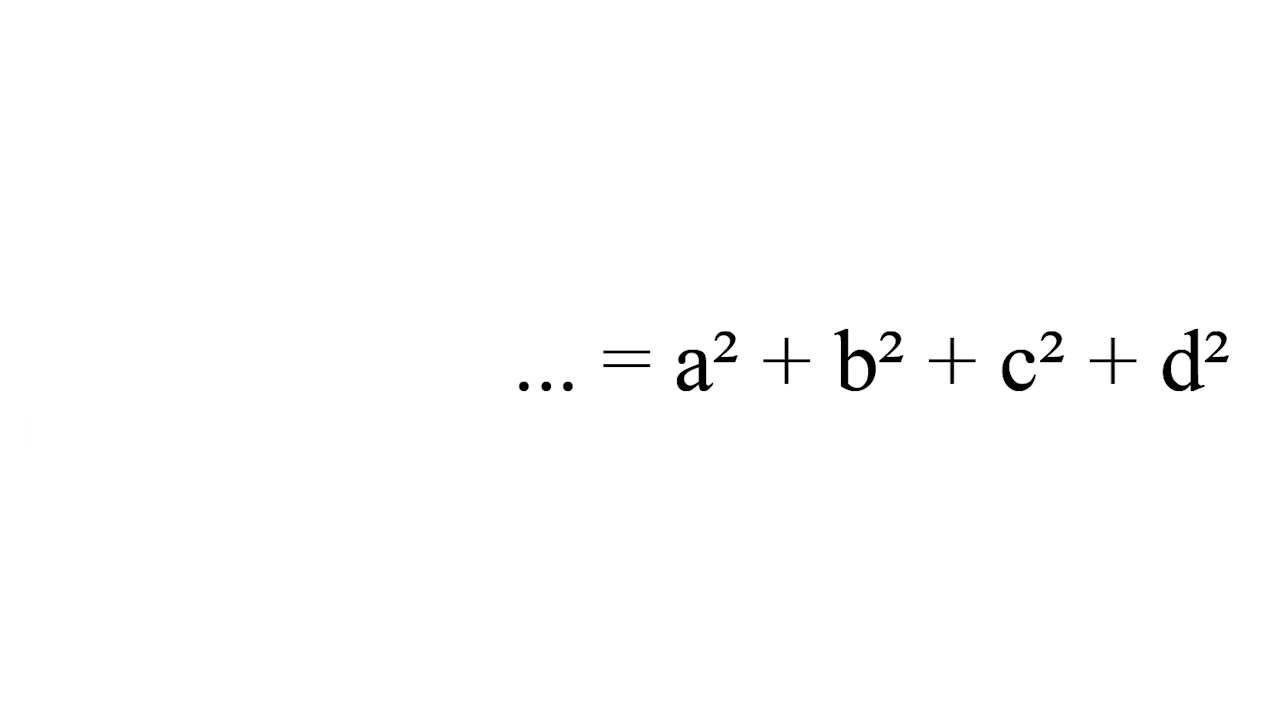
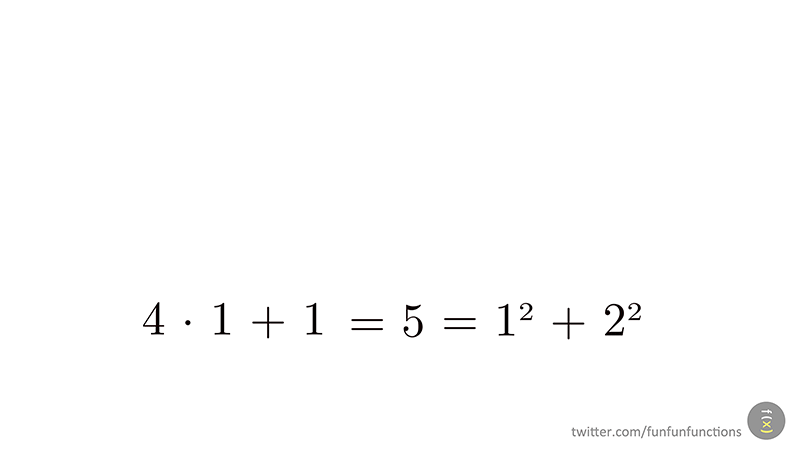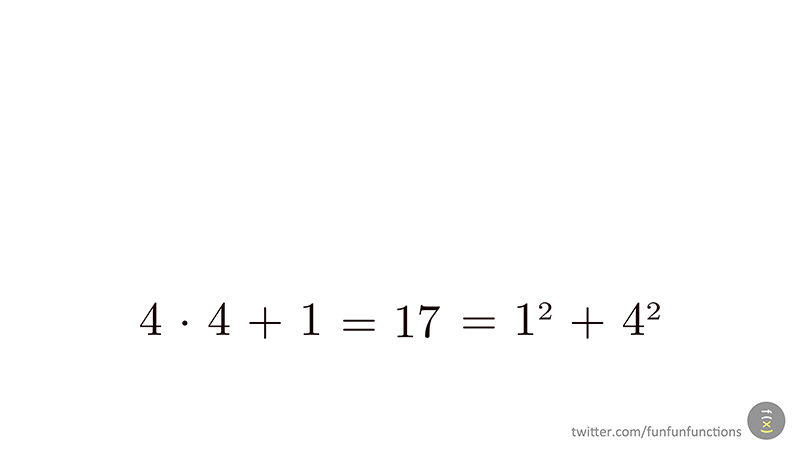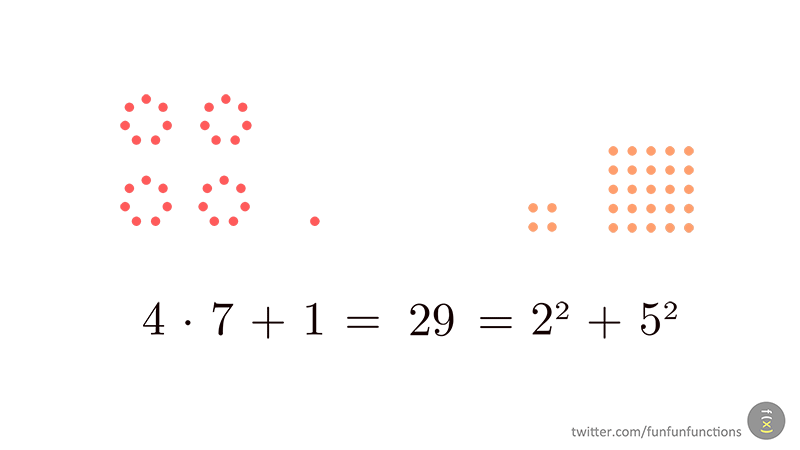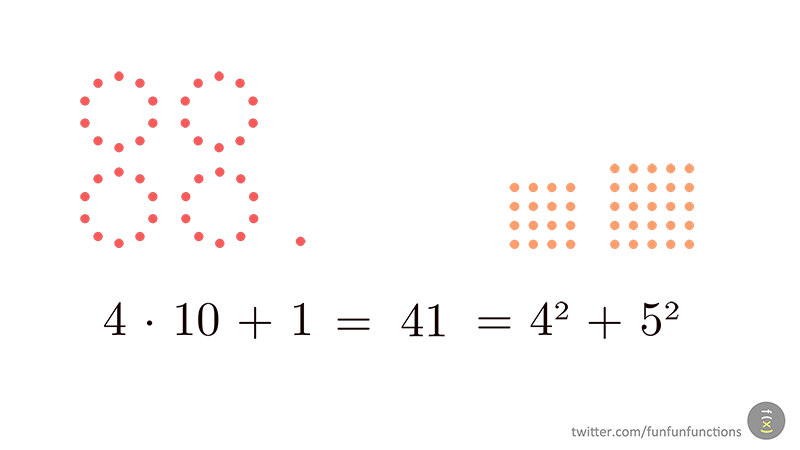
Cap comentari:
Publica un comentari a l'entrada