Patrons a les taules de multiplicar

Ja vam tractar aquest tema als posts Més activitats relacionades amb la graella del 100 i Graella multiplicativa i especialment a l'article: "Tareas ricas para practicar las tablas" de la secció "Ell@s tienen la palabra" que escrivim a cada número de la revista SUMA.

El patró més famós que podem comentar sobre la taula del 9 ja el va presentar Miliki:

I d'aquest patró deriva un truquet que molts dels nostres alumnes utilitzen per memoritzar la taula i que nosaltres podem ajudar-los a entendre d'on surt.

En la xerrada que va fer el John Mighton en Barcelona l'1 de març també es va comentar la importància d'analitzar a l'aula els patrons que amaguen les taules per ajudar a la seva memorització. Justament inspirat en una proposta de Jump Math en el blog Mathrecreation trobem el post Squashing multiples on s'anailitzen els patrons que resulten de sumar els dígits del resultat d'una multiplicació fins a aconseguir un nombre d'una xifra (per exemple, el resultat de 8x7 = 56 i a partir d'aquest resultat fem: 5+6=11 → 1+1=2)

En la imatge següent del post abans esmentat es veu el patró resultant de sumar dígits en els resultats de les taules del 3, del 6 i del 12:

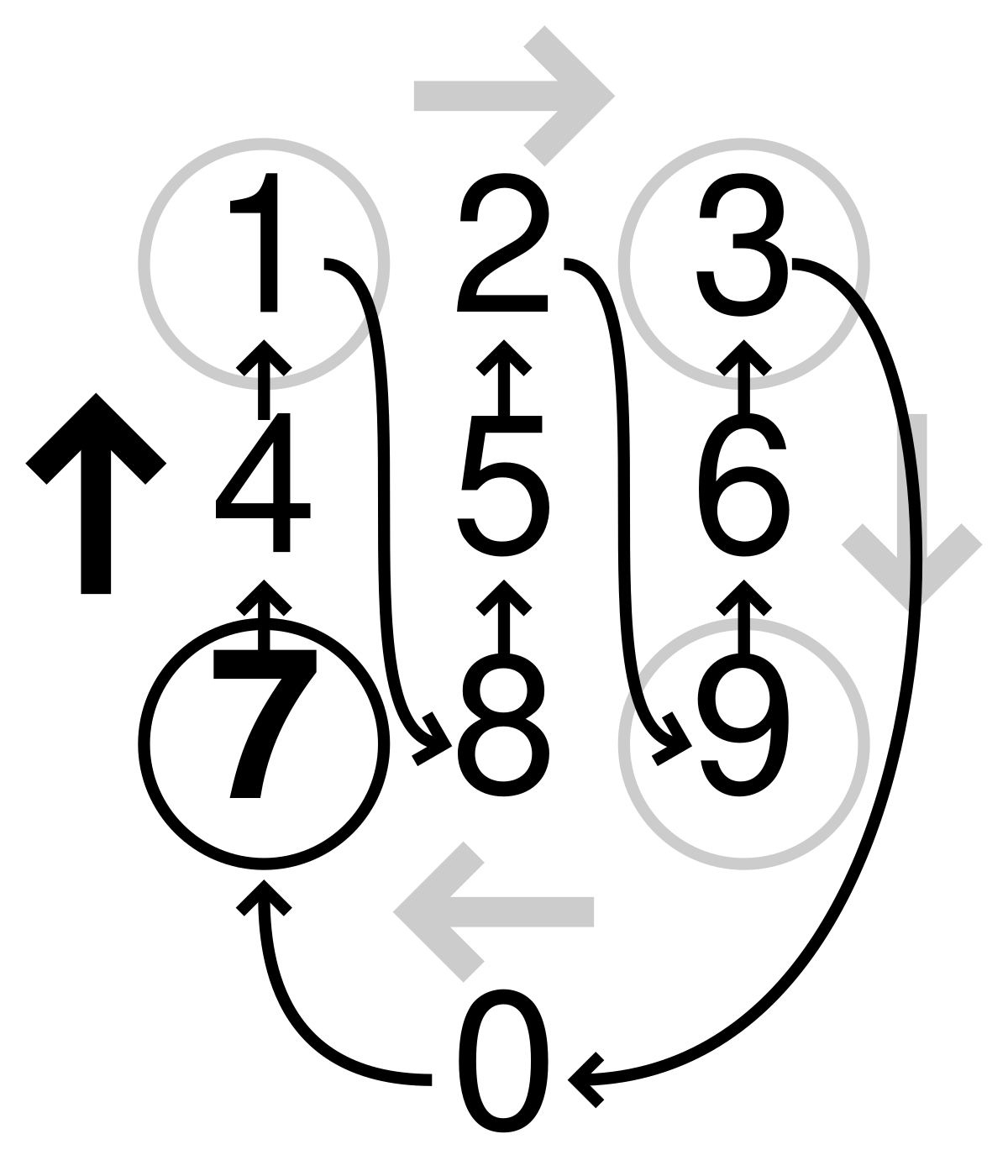
A la Wikipedia trobem un patró curiós relacionat amb la taula del 7:

• Sortim del 7
• El següent nombre seguint la fletxa és 4 i el primer nombre major que 7 que acaba en 4 és 14
• El següent número seguint la fletxa és 1 i el primer nombre major que 14 que acaba en 1 és 21
• El següent número seguint la fletxa és 8 i el primer nombre major que 21 que acaba en 8 és 28
• ...

By Cmglee - Own work, CC BY-SA 3.0, Link

El @jimmybcn2 explica en el post Patterns in tables una d'aquestes tasques analitzant patrons amb alumnes de 3r de primària. Allí comenta que va partir de la proposta de @Nrich Tables Without Tens i la va complementar amb una adaptació del vídeo de @mickaellaunay La face cachée des tables de multiplication

Cada cercle correspon a una taula i en cada cercle apareixen els nombres del 0 al 9, els alumnes havien d'unir cada nombre amb la xifra de les unitats del resultat (per exemple, en el cercle de la taula del 6 els 3 s'uneix amb el 8 perquè 3x6 acaba en 8). Aquí hi ha dos mostres del que van fer els alumnes:

I aquí una plantilla per si voleu proposar aquesta tasca als vostres alumnes.

La Laia Fonts i el Daniel Solera de l'escola Josep Maria Jujol de Gràcia van proposar als seus alumnes de 3r de Primària que analitzessin uns altres patrons presents a les taules. 

Aquí també cada cercle correspon a una taula i en cada cercle apareixen els nombres del 0 al 9, però els alumnes havien d'unir nombres seguint la sèrie que descriuen les xifres de les unitats dels resultats d'aquesta taula (per exemple, en el cercle de la taula del 6, s'uneix el 6 amb el 2, aquest amb el 8, després amb el 4, amb el 0 i per últim amb el 6 perquè els resultats de la taula del 6 acaben en 6, 2, 8, 4, 0, 6, 2, 8, 4, 0,...). Ho van fer sobre rodes, després ho van passar a paper i per últim van descriure les seves conclusions!!

El @jimmybcn2 després de veure aquesta proposta va ampliar la que havia fet als seus alumnes de 3r de @escolasadako obtenint resultats igualment bons (ho explica en el post Even more patterns in tables)