Resolució d'equacions amb una balança

Els models més utilitzats per donar significat a la relació abstracta entre símbols que estableix una equació són: el model aritmètic, la balança i el model geomètric (B.A. van Amerom presenta aquests tres models en la seva tesi: "Reinvention of early algebra. Developmental research on the transition from arithmetic to algebra" Utrecht University, 2002).

En un post anterior d'aquest bloc (Resolució d'equacions amb "cover up") vam referir-nos a l'ús del model aritmètic per treballar les equacions i vam presentar un applet relacionat amb aquest model. En aquest post farem el mateix amb el model de la balança.

Aquest model es basa en la representació d'una equació com l'equilibri d'una balança de dos plats sobre els quals hi ha objectes de pes conegut i un o més objectes iguals però de pes desconegut que volem conèixer.

• Per representar en aquest model l’equació 3·x + 2 = x + 8, en un dels plats de la balança, posem tres paquets iguals però de pes desconegut i una pesa de dos quilos i en l'altre plat posem un paquet igual als altres tres i una pesa de vuit quilos, de manera que la balança queda equilibrada.

• Per donar sentit a cada pas de la resolució d'una equació com aquesta ens aprofitem de la pròpia balança sobre la qual es troben els paquets i les peses: traiem primer dos quilos de cada plat romanent la balança equilibrada, traiem un paquet de cada plat sense que s'alteri l'equilibri i per últim, eliminem la meitat del contingut de cada plat, resultant que en un plat queda només un paquet i el seu pes és de 3 quilos.

Un applet que reflecteix a la perfecció aquest model és la "Balanza Algebraica" inclòs en la "Biblioteca de materiales manipulativos virtuales" de la Universitat de l’Estat de Utah. La limitació més gran que té aquest model és la dificultat per representar equacions amb coeficients negatius o amb solucions negatives. Però la “Biblioteca de materiales manipulativos virtuales” proposa una solució per aquesta limitació amb una altra aplicació interactiva: "Balanza Algebraica – Negativos". Encara que aquests dos applets no estan actualment disponibles directament Rafael Lozada va recrear-los aquí: "La balanza (naturales)" i "La balanza (enteros)"

Si bé és cert que aquesta estratègia només permet resoldre equacions de primer grau de la forma ax + b = cx + d, les transformacions realitzades sobre els plats de la balança que permeten passar d'una equació a una altra equivalent, es poden generalitzar. D'aquesta manera es poden continuar explicitant les transformacions realitzades entre una equació i una altra més senzilla com si sempre s'estigués davant d'una balança. Es poden així abandonar regles mnemotècniques buides de sentit i provocadores de greus errors com són "si està sumant passa restant" o "si està dividint passa multiplicant".

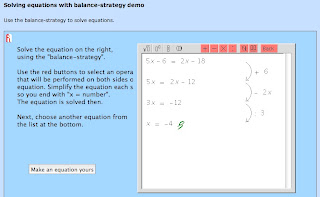
Els applets dissenyats pel ja esmentat Freudenthal Institute: "Solving equations with balance-strategy: demo" i “Solving equations with balance-strategy: game” estan impregnats de la idea del paràgraf anterior. La diferència entre els dos applets rau que mentre que en el primer el treball de l'alumne consisteix únicament a indicar a l'ordinador que transformació vol realitzar, en el segon a més de donar aquesta ordre ha d'indicar el resultat d'aquesta transformació.

La possibilitat de treballar amb aquests dos applets permet al mestre separar el treball de manipulació algebraica, amb el qual molts alumnes tenen dificultats, del treball de transformació d’equacions pròpiament dit. L’ús d’aquests applets també suggereix una manera d’enregistrar el raonament que hi ha darrere de la resolució.

Aquesta imatge ensenya com una alumna enregistra la resolució d’una equació de primer grau després d'haver utilitzat els applets descrits.

Un altre exemple en el qual es veu que l’alumne en escriure “-2kg” està pensant en termes de l’applet “Balanza Algebraica”

Un exemple que involucra parèntesis i en el qual es veu com l’alumna fa servir les mateixes icones que l’applet “Solving equations with balance-strategy”, en particular, una icona amb dos parèntesis tatxats per indicar la propietat distributiva, o sigui, la simplificació de l’expressió algebraica

Un exemple que involucra denominadors en el que novament s’aprecia l’ús d’icones inspirades per l’applet: dos quadrets amb una clau a sota per indicar que combinarà termes semblants.

Els alumnes van conservar les pràctiques aquí esmentades en les sessions dedicades a l’aplicació d’equacions per resoldre problemes en context. En les següents imatges es pot apreciar com es manté la manera d’enregistrar el procés de resolució d’equacions:

Un exemple de com l’estratègia és aplicada a la resolució de problemes

Amb els temps alguns alumnes ja han deixat de representar les fletxes per indicar cada transformació. Aquesta modificació es considera natural en la mesura que tota bastida es desmunta quan l’obra ja està acabada.