Per començar el tema recomanem llegir la introducció que fa el Joan Jareño a la seva proposta "Tirem els daus" on comenta la història i diferents tipus de daus. Destaquem altres dos apartats d'aquesta proposta:
- "Un dau carregat" on analitza com es pot saber quin nombre és afavorit per aquesta deformació.
- "Per què no em surt el cinc?" on analitza les ratxes de "mala sort"
Se coloca una ficha en la casilla indicada como "salida" y se lanza un dado dos veces. en cada ocasión, si sale 1, 2 o 3, se avanza una casilla y se sube otra. Pero si sale 4, 5 o 6, se avanza una casilla y se baja otra. Después de introducir el juego es momento de que conjeturen, experimenten y tomen la palabra para discutir: ¿en qué casillas puede acabar el recorrido?, ¿en cuál de ellas es más probable que acabe? Si hacemos el experimento unas 900 veces, ¿cuántas veces cabe esperar que acabe en cada una de las casillas? Es interesante analizar cómo afecta a las respuestas anteriores el hecho de realizar pequeños cambios en las reglas del juego. Para ello planteemos una segunda versión de éste: sólo cambia que avanzo una casilla y subo una casilla cuando en el dado sale 1, pero si sale cualquier otro número después de avanzar una casilla, bajo una. en esta nueva versión del juego, las casillas en las que puede acabar el recorrido son las mismas (F, H y J) pero ahora la más probable ya no es la H, sino la J.
Una tercera versió d'aquest joc passa per avançar una casella i pujar-ne una altra quan al dau surt un 1 o un 2 i avançar una casella i baixar-ne una altra quan surt un 3, un 4, un 5 o un 6. En aquest cas és igualment probable acabar el recorregut en la casella H o en la J (4 entre 9 en cada cas). Encara que hi ha una certa probabilitat d'acabar el recorregut en la casella F (1 entre 9) però no es lògic apostar per acabar allí a menys que el premi compensi el risc. Podem proposar als alumnes que reflexionin sobre les raons per les que continuaria sent poc raonable apostar per la casella F encara que el premi per encertar quan s'aposta per la casella F és el doble (o, fins i tot, el triple) que quan s'aposta per les caselles H o J.
Aquesta idea de canviar els premis per equilibrar jocs en els quals els resultats no són igualment probables també ha estat explorada en algunes de les activitats del Proyecto Gauss. Un exemple molt interessant en aquest sentit és el de la "Ruleta de Frutas" que estudia a quin preu s'ha de cobrar el dret a jugar els organitzadors si no volen perdre diners.
Dos daus
A l'article de SUMA esmentat abans vam desenvolupar un joc que ben podria formar part del post anterior: Parells i senars.
Tenemos muchas situaciones en la que dos niños deben repartirse dos tareas una de las cuales es la preferida por ambos, en esos casos se les puede proponer que lo echen a suertes con los dados. El juego podría ser el siguiente: uno de ellos elige par o impar, se tiran dos dados, se multiplican los dos números y se mira si el resultado tiene la paridad elegida, si acertó elige la tarea que prefiere sino la elige el otro niño. Podemos preguntar a la clase si conviene elegir par o impar [...] Y ¿qué sucedería si en lugar de multiplicar los resultados de los dos dados los sumáramos?
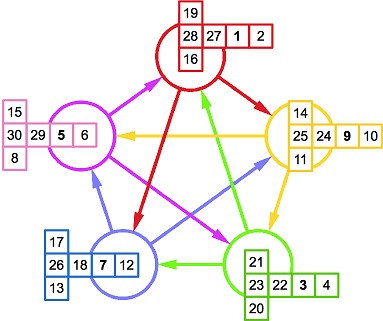
Van aprofitar aquest exemple per destacar la importància de les taules de doble entrada per analitzar-los i ara podem afegir un altre exemple en que aquestes taules demostren la seva utilitat: els daus de Sicherman, que apareixen a la imatge següent, tenen la propietat de generar la mateixa probabilitat que dos daus convencionals d'obtenir resultats entre 2 i 12 quan es sumen els dos valors obtinguts en llançar-los (més informació aquí).
Volem recordar aquí l'activitat dissenyada per fer en grups a la prova de Competències bàsiques a l'ESO proposada a l'any 2006 (la podeu trobar aquí: el quadern individual i el quadern del grup). Es tracta d'una activitat en que es proposa a cadascun dels integrants del grup tasques específiques per realitzar amb dos daus (han de llançar-los i enregistrar el resultat de la suma, la resta, la multiplicació i el màxim dels dos valors obtinguts) i que al nostre entendre permet explorar molt bé les idees que tenen els nostres alumnes sobre la probabilitat abans de fer servir les taules de doble entrada.
Tres daus i més
Tres daus i més
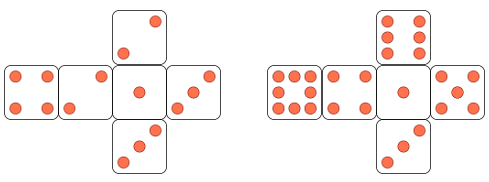
En relació a activitats on s'involucra l'ús de tres daus us recomanem aquesta simulació del joc "pedra, paper i tisores"
 |
| https://mathsgear.co.uk/products/non-transitive-grime-dice |
| Les cares que no es veuen tenen el mateix valor que les oposades visibles a la imatge. Font: http://es.wikipedia.org/wiki/Dados_no_transitivos |
 |
| http://singingbanana.com/dice/articleold.htm |
Per acabar, alguns comentaris més
- a continuació podeu veure un fantàstic vídeo del James Grime on, fins i tot, es pot trobar un joc amb cinc daus d'aquest tipus
- De daus no transitus també es parla a Un extraño juego de dados. A més de gràfics molt guapos s'afegeix una altra característica que diferencia el joc amb daus del joc pedra, paper i tissores (la primera diferencia és que amb els daus no hi ha empat). Si tres persones juguen simultàniament ni pedra, ni paper, ni tissora té major probabilitat de guanyar però si tres daus juguen simultaniament hi haurà un que té més probabilitat que els altres de guanyar.
- Dels 10 esdeveniment possibles en pedra, paper, tissores jugats entre tres persones (r=pedra, p=paper,t=tissores) rrr, ppp, ttt i rpt: generen empats rtt, tpp, prr: hi ha un guanyador, el que tria una cosa diferent trr, ptt, rpp: hi ha un perdedor, el que tria una cosa diferent, però no hi ha guanyador
- Dels 216 esdeveniments possibles en el llançament dels tres daus utilitzats a http://www.teachmaths-inthinking.co.uk/activities/grime-dice.htm El vermell guanya amb 9xy i 420 (1x6x6+5x3x1=51 del 216 casos possibles) El blau guanya amb 47 y (5x3x6=90 del 216 casos possibles) El verd guanya amb 425 (5x3x5=75 del 216 casos possibles) O sigui que el blau té un 41% de probabilitat de guanyar als altres dos, mentre que la probabilitat del verd és del 35% i del vermell només un 24
- Val la pena l'entrada que sobre aquest tema ha publicat el Joan Jareño al seu blog Calaix

- Cut the knot presenta el treball de Bráulio de O. Silveira en relació a l'existència de set conjunts de cinc daus no transitius
 |
| http://www.cut-the-knot.org/Probability/Nontransitive-Dice-5.pdf |
Encara que no té a veure amb probabilitat, al mmaca ens presenten una altra situació d'ordre "no transitiu"


Trobareu una altra activitat sobre probabilitat i suma de daus a http://wordplay.blogs.nytimes.com/2013/06/24/dice/
ResponEliminaMuy interesante.
ResponEliminaEatoy aprendiendo
Ricardo