Partim de la idea que desprès de treballar junts, discutir col·lectivament, i entendre les coses des del context, els alumnes assoleixen de diferent manera el tema tractat. Per tancar el procés cal realitzar un treball que indiqui als alumnes i els seus mestres el grau d'assoliment individual del tema tractat. Vist des del punt de mira actual això ha de servir per reflexionar i ser conscients de la millora personal de cadascú. Com diu Neus Sanmartí "no hi ha res més engrescador que tenir la sensació que aprens". L'autocorrecció pot ajudar als alumnes a controlar aquest procés de millora.
Posats en aquest context plantegem la pregunta eterna: els alumnes han de disposar dels resultats dels exercicis? Per què als llibres de text no hi apareixen? A aquesta última pregunta s'hauria d'afegir "al nostre país" ja que, per exemple, el llibre (de text) "La Geometria" de Emma Castelnuovo, a la seva edició de 1970, presenta molts dels exercicis proposats, amb el resultat incorporat.
 |
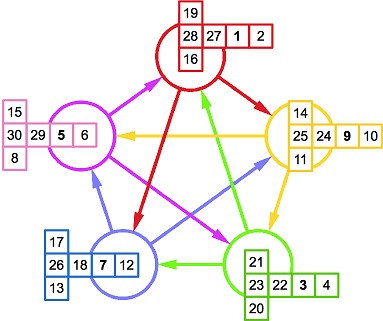
| Con es veu a la imatge tots els problemes menys el 22 i el 23 donen el resultat |
Hi ha una llarga tradició de propostes de materials autocorrectius, des de fa molts anys. I també de nova creació. En presentem un quants:
Capses Heinevetter
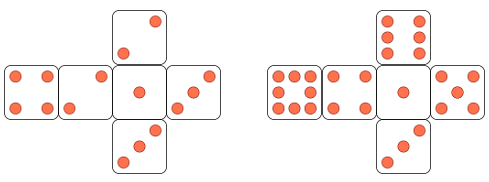
 Podríem dir que la idea d'autocorrecció ha estat present des de fa molt, en poden ser exemples: el treball de Freinet o materials específics que van sortir al mercat a la dècada del 70. "Heinevetter" és un d'aquests materials: unes capses amb taules en que en cada cel·la es proposa una "pregunta", sobre cada cel·la s'ha de posar una peça de puzle que contingui la resposta numèrica corresponent. L'autocorrecció està basada en que les peces encaixen quan les respostes són correctes.
Podríem dir que la idea d'autocorrecció ha estat present des de fa molt, en poden ser exemples: el treball de Freinet o materials específics que van sortir al mercat a la dècada del 70. "Heinevetter" és un d'aquests materials: unes capses amb taules en que en cada cel·la es proposa una "pregunta", sobre cada cel·la s'ha de posar una peça de puzle que contingui la resposta numèrica corresponent. L'autocorrecció està basada en que les peces encaixen quan les respostes són correctes.L'exemple de la imatge és de comptatge i identificació de numerals però hi ha una extensa varietat de capses que treballen diferents nivells i aspectes. Més informació: EJE
Capses ARCO
Material força conegut al nostre país, també treballa amb peces que cal col·locar en una base. La diferència està en la dinàmica: els alumnes posen les "peces resposta" sobre la pregunta. Es tanca la capça, se li dona la volta i en obrir per l'altre costat, si les respostes són correctes ha de sortir una sanefa. Si no surt queda clar on estan les equivocacions. Més informació: EJE.
 | ||
| Les dues peces de color mostren la part del darrera que crea la sanefa |
Claus d'aprenentatge ARCO
Enfocades bàsicament a aprenentatges d'habilitats, com per exemple sumes de dígits o taules de multiplicar tal i com s'ensenya en aquest vídeo. En acabar de passar el fil per les solucions correctes, en donar la volta el fil ha de seguir un camí marcat a la part del darrere. Més informació: EJE
 |
| Materialització de "Claus d'aprenentatge" realitzada pels mestres de la Skogsbackeskolan (Karlstad, Suècia) |
Tot i que fins ara això de l'autocorrecció sembla més aviat un relat històric, no és així. Actualment hi ha propostes noves que continuen sortint al mercat, com per exemple les propostes de "K2 publishers" malauradament, per nosaltres, escrites en holandès. Els tipus d'activitats proposades, són molt interessants en general i responen a la manera de fer actual. Podria ser un bon material per a un racó d'aprenentatge. Us presentem una activitat de "vistes".
 |
| Tal com es veu al primer exemple els nombres de les graelles indiquen l'altura de cadascuna de les torres. |
L'autocorrecció funciona posant un plàstic transparent vermell als requadres de la dreta i així es visualitza el resultat. Per facilitar la visió d'aquests resultats el material disposa d'un artefacte com el següent. Mireu-ne el funcionament a la imatge.
Autocorrecció com a ambient de classe
Independentment dels materials involucrats l'autocorrecció, el tema està en la decisió de si la integrem o no al funcionament normal de les nostres classes. Imaginem un full d'operacions on l'exercici final fos:
Independentment dels materials involucrats l'autocorrecció, el tema està en la decisió de si la integrem o no al funcionament normal de les nostres classes. Imaginem un full d'operacions on l'exercici final fos:
- comprova els resultats (amb la calculadora o amb un llistat de solucions adjunt);
- marca les errades que has fet;
- en un parell d'aquests casos, explica en què t'has equivocat.
El post "autocorrectius" no s'acaba aquí us convidem a seguir llegint el paper de les noves tecnologies en l'autocorrecció en el post "Autocorrectius 2" que penjarem en un parell de dies.