Aquesta tasca està inspirada en el problema anomenat Diffy que ja vam comentar al post Pràctica productiva i pràctica reproductiva però amb una formulació diferent, més propera a l’estudi realitzat pel matemàtic E. Ducci en 1930 que va trobar que sense importar els nombres d’inici sempre s’arriba a quatre zeros (Font: Cut the knot)
Al "Cuaderno de Cultura Científica" la @MartaMachoS ha fet un article sobre "El teorema de Ducci" que ens ha permès conèixer una sèrie molt interessant de referències sobre aquest problema. Entre elles destaquem Carlos D’Andrea y Adrián Paenza, Un cuadrado, cuatro números, Pensamiento matemático vol VIII, no. 1, 71-82.
Farem diagrames amb les normes següents:
- en totes les files hi ha 4 cel·les en cada cel·la,
- a partir de la segona fila, has d’escriure la diferència entre les dues cel·les que té immediatament a sobre
- en el cas de l’última cel·la de cada fila la diferència l’has de fer entre el últim i el primer nombre de la fila anterior
- el diagrama acaba quan en tota la fila s’obtenen zeros
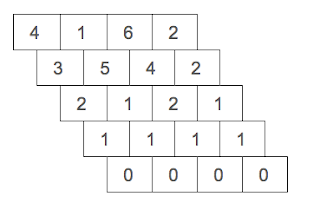
Exemple: començant amb els nombres 4, 1, 6 i 2 el diagrama té 5 files
Els alumnes als que vam proposar el repte no van aconseguir diagrames de més de 8 files (val a dir que van trobar moltes quaternes diferents que generaven diagrames d’aquesta mida) possiblement perquè a partir de l'exemple, van creure que els nombres inicials havien de ser menors que 10.
El @rbalague11 ens va regalar aquest petit applet per experimentar amb diferents quaternes de dígits!!
En el context del projecte Problemàtiques alguns mestres del departament col·laboratiu de Matemàtiques de la @FTrams vam proposar a alumnes del cicle superior de Primària que triessin nombres de la primera fila perquè el diagrama tingués la major quantitat de files que puguessin aconseguir. L'activitat va ser un èxit, ja que va engrescar molt als alumnes.
A la següent imatge podeu veure l'anàlisi d'una alumna sobre com afecta l'ordre dels nombres de la primera fila a la quantitat de files del diagrama
En aquesta línia, alguns alumnes van voler analitzar totes les 24 possibles distribucions dels 4 nombres en la fila inicial, sense adonar-se que, per simetries i girs, en realitat només cal estudiar tres distribucions diferents i no més.Els alumnes als que vam proposar el repte no van aconseguir diagrames de més de 8 files (val a dir que van trobar moltes quaternes diferents que generaven diagrames d’aquesta mida) possiblement perquè a partir de l'exemple, van creure que els nombres inicials havien de ser menors que 10.
El @rbalague11 ens va regalar aquest petit applet per experimentar amb diferents quaternes de dígits!!
Introdueix els quatre nombres inicials (entre 1 i 9)
Nombre de la posició 1:
Nombre de la posició 2:
Nombre de la posició 3:
Nombre de la posició 4:
Però el cert és que, si permetem que a les cel·les vagin nombres majors que 9, hi ha diagrames de tantes files com es vulgui. Per exemple:
- començant amb els nombres 1, 15, 30 i 60 el diagrama té 10 files
- començant amb els nombres 0, 653, 1854 i 4063 el diagrama té 24 files
- Es pot preguntar quin és el diagrama en el que aconsegueixin que hi hagi nombres senars en major quantitat de files. El cert és que a partir de la cinquena fila mai queden nombres senars però es poden triar quaternes en que quedi algun senar fins a la 4a fila (per exemple: 2 4 6 7 → 2 2 1 5 → 0 1 4 5 → 1 3 1 3 → ...) Font: D. Shapiro
- Es pot proposar als alumnes que analitzin el joc quan en lloc de diagrames que tenen 4 nombres per fila en tenen altres quantitats. La conclusió de que sempre s’arriba a tots zeros pot deixar de ser certa Per exemple, per diagrames de 3 nombres per fila es pot entrar en un bucle 1 2 2 → 1 0 1 → 1 1 0 → 0 1 1 → 1 0 1 → 1 1 0 → 0 1 1... Acabem sempre amb el cicle aa0 → a0a → 0aa on a és el mcd dels nombres diferents de zero de la primera fila.
- Es pot demanar als alumnes que comparin un diagrama i el que resulta de sumar, restar o multiplicar a tots els nombres de la quaterna inicial per un mateix nombre.
- Don Steward proposa comprovar que si els 4 nombres inicials estan en progresió aritmètica la quantitat de files és sempre la mateixa (6), investigar què passa quan els 4 nombres inicials són quadrats consecutius, són nombres triangulars consecutius, són termes de Fibonacci, etc o estudiar què passa si a tots els nombres de la quaterna els multipliquem o els sumem un mateix nombre
- Es pot demanar als alumnes que per a la quaterna inicial triïn nombres que no siguin enters. En aquest sentit, a 4t d'ESO de @escolasadako, aquest any vam proposar als alumnos experimentar amb nombres irracionals
Val la pena analitzar que la petita quantitat de files també es dóna quan totes les entrades són irracionals. Aquí veiem l'anàlisi de la situació amb tres irracionals:
A la dreta apareixen les aproximacions decimals dels valors de cada cel·la per guiar la decisió de quin nombre és més gran i així decidir si es resta a-b o b-a.
El Josep, alumne del Màster de Secundària (grup 3, curs 18-19) ho va comprovar utilitzant els quatre irracionals més famosos
El Sergio B. (@magiaymates) es va preguntar: I per què no aplicar això per practicar restes de polinomis? Només haurem de decidir que vol dir fer la diferència entre dos polinomis...
A continuació apareix un exemple entenent que fer la diferència entre dos polinomis és fer la resta entre ells en l'ordre que permeti que el coeficient principal (el del terme de major grau) del resultat sigui positiu.
El Josep, alumne del Màster de Secundària (grup 3, curs 18-19) ho va comprovar utilitzant els quatre irracionals més famosos
El Sergio B. (@magiaymates) es va preguntar: I per què no aplicar això per practicar restes de polinomis? Només haurem de decidir que vol dir fer la diferència entre dos polinomis...
A continuació apareix un exemple entenent que fer la diferència entre dos polinomis és fer la resta entre ells en l'ordre que permeti que el coeficient principal (el del terme de major grau) del resultat sigui positiu.