Pràctica productiva: restes (4)

A partir de que els alumnes sàpiguen fer restes en el rang 0-100 els podem presentar aquesta tasca, inspirada en "Monty the Python" una tasca publicada per l'ATM a "Rich Task Maths 1" (2011): "Hem dibuixat cinc serps sobre la graella del 100. La longitud d'una serp es calcula comptant quantes cel·les ocupa i el seu pes, fent la diferència entre els nombres que estan al cap i a la cua de cada serp. Les cinc serps dibuixades tenen longitud 7 però, quant pesa cadascuna?" 

Encara que no és imprescindible diferenciar els dos extrems, per simplificar la comunicació direm que el cap és, dels dos extrems, el que conté el menor nombre i el cap, l'altre.

No hi ha misteri en el càlcul del pes de les serps rosa, taronja, verda o groga. El problema es presenta al moment de calcular el pes de la serp blava: el cap és el 18, però quina és la cua? el 29? el 38? el 40?. Els tres nombres poden ser la cua!! i aquí tenim la primera oportunitat per plantejar un repte als alumnes: trobar totes les serps que s'amaguen en aquesta imatge blava i els seus pesos.

Tres serps de formes diferents però amb la mateixa "silueta"

Atenent a aquesta distinció entre forma i silueta podem demanar maneres de representar una serp perquè no quedi dubte de com és la seva forma ni on està ubicada. Per exemple, la primera de les tres serps de l'última imatge podria representar-se així: 18, 28, 38, 39, 40, 30, 29.

Però hi ha moltes més preguntes amb les que podem enriquir aquesta activitat: 

• Pensant en serps de longitud 7 podem preguntar-nos: quant pesen les serps més pesants? quina forma tenen? Però és molt més interessant pensar en les serps més lleugeres... Totes les serps de pes 60 tenen la mateixa forma (la de la serp rosa de la imatge inicial) però les serps de pes 2 poden tenir formes molt diferents. A continuació aprofitem un applet de math_bot per ensenyar serps de longitud 7 i pes 2 però amb diferents siluetes: 

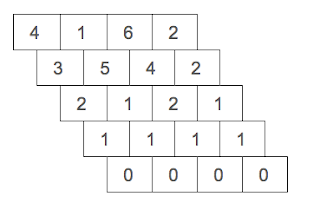
• Com canvia el rang de pes de les serps en funció de la seva longitud? Aquesta taula fa intuir interessants patrons i provoca fer-se noves preguntes (què més podem demanar a una taula?)

Aquesta taula substitueix una altra que els companys del 

CEIP Sant Jordi de Palma van detectar que contenia errades:

el pes mínim d'una serp de longitud senar pot ser 1!

Aquí es veu una serp de longitud 11 i una 

altra de longitud 33, totes dues de pes 1.

• Si 26 és el cap d'una serp de longitud 5, on pot estar la seva cua?

Observar que el fet d'haver fixat que el cap és l'extrem amb
menor valor evita que les solucions d'aquesta pregunta
incloguin als nombres 24, 22, 19, 17, 15, 13, 8, 6 i 4  

• Quins són tots els pesos possibles per a les serps de longitud 6? Sabem que el pes mínim és 1 i el màxim és 50 però quins valors entre 1 i 50 són efectivament pesos de serps de longitud 6?

Podem començar pensant on pot estar la cua d'una serp de longitud 6, que tingui el cap, per exemple al 5 i a partir d'allí pesar les serps per ariibar a que els pesos possibles són 1, 3, 5, 6, 8, 10, 12, 14, 17, 19, 21, 23, 28, 30, 32, 39, 41 i 50!! 

Observar que aquí no perdem solucions per demanar que el cap tingui un valor
més petit de la cua (perdem serps, per exemple, 5-15-25-24-14-4, però no perdem
pesos possibles ja que ja tenim una serp de pes 1: la que té el cap al 5 i la cua al 6)

Però això només és l'inici. Se'ns obre un ventall enorme de preguntes que encara no ens hem fet: quina és la serp més llarga que no toqui a cap nombre parell? i a cap primer? i a cap quadrat?

Una serp de longitud 19 que no toca cap múltiple de 3

Qui és l'intrús?

Una de les taques amb més èxit durant les trobades de formació de mestres són les QUELIs. Els mestres de seguida veuen el seu potencial per fer parlar als alumnes i intueixen com s'engrescaran els alumnes buscant arguments per defensar les seves respostes. O sigui, les QUELIs són tasques ideals per valorar les dimensions "comunicació i represantació" i "raonament i prova".

Què són les QUELIs?
Per explicar què significa QUELIs o WODB i quines característiques tenen aquestes tasques, per comentar com podem portar-les a l'aula i quines variants hi ha creiem que el millor es remitir-vos al resum de la presentació que van fer @davidobrador i @ccbcnmvd al C2EM 2016:

Exemples de QUELI's
Hi ha exemples per a totes les edats i relacionades amb tots els blocs temàtics. A més de la pàgina "oficial" que recull exemples d'aquestes tasques: http://wodb.ca, a Twitter, sota l'etiqueta #wodb els usuaris comparteixen les que dissenyen ells i les que proposen en les seves aules:

Comentarem la nostra experiència amb tres QUELIs de geometria que vam portar a l'aula

Anomenarem A a l'objecte que està a dalt a l'esquerra, B el que està a dalt a la dreta, C el que està a baix a l'esquerra i D a l'últim

Amb aquesta proposta surten arguments relacionats amb

• els eixos de simetria: B és l'intrús perquè és l'únic que les diagonals són eixos de simetria o C és l'intrús perquè és l'únic que té un únic eix de simetria o D és l'intrús perquè és l'únic que no té cap eix de simetria  
• les diagonals: A és l'intrús perquè és l'únic que té les diagonals iguals tallant-se al punt mig o  és l'intrús perquè és l'únic que té diagonals perpendiculars o C és l'intrús perquè és l'únic que les diagonals no es tallen al punt mig
• els costats: C és l'intrús perquè és l'únic que té tres costats de mides diferents o A és l'intrús perquè és l'únic que té costats perpendiculars o B és l'intrús perquè és l'únic que té tots els costats igual
• els angles: A és l'intrús perquè és l'únic que té tots els angles iguals o C és l'intrús perquè és l'únic que té un angle obtús oposat a un angle agut
• ... 

Aquí també els arguments han estat variats

• A és l'intrús perquè és l'únic acutangle, o l'únic que té com a eix de simetria la diagonal del geoplà
• B és l'intrús perquè és l'únic escalè, o l'únic que té un costat de longitud major que 4
• C és l'intrús perquè és l'únic rectangle o l'únic que la seva frontera només té contacte amb tres punts del geoplà
• D és l'intrús perquè és l'únic que no té punts del geoplà a l'nterior, o l'únic que té un costat de longitud 4

En aquest cas, a més de convidar als alumnes a exposar arguments sobre perquè cadascuna de les figures era "l'intrusa" vam plantejar que pensessin què tenien en comú les peces vermelles, les verdes i sobre tot les blaves. El fet de reconeixer que el mateix color indicava mateixa àrea els va donar nous arguments: C és l'intrús perquè és l'únic que té àrea 9 triangles verds o D és l'intrús perquè és l'únic que té àrea 8 triangles verds.

A la fase final del Fem Matemàtiques 2019 l'organització va proposar als participants com a activitat inicial per formar grups puzzles relacionats amb #QUELIs (a cada participant es lliurava amb la inscripció una imatge que corresponia a la cinquena part d'una imatge major que corresponia a una tasca del tipus "qui és l'intrús?" havien de juntar-se amb la resta de participants que tenien imatges de la mateixa QUELI i entre tots argumentar les quatre opcions)

Tasques riques i Fibonacci

La successió de Fibonacci (una successió en que cada terme és la suma dels dos anteriors) és una font inesgotable de tasques riques. En aquest post comentem tres exemples.

Tasca 1

Aquí tenim un exemple proposat en Cicle Inicial on l'objectiu és practicar de manera productiva sumes en el rang 0-100:

"Laboratori de nombres" (1r Primària, Innovamat)

A diferència del primer apartat de la tasca en que la solució en cada cas és única (encara que les estratègies que demanen no és la misma en els quatre casos)

• a l'apartat 2 es demanen dues de deu solucions possibles (en les primeres dues cel·les es poden col·locar els nombres 1-10. 2-9, ..., 10-1) Val a observar que els cucs generats en col·locar en les dues primeres cel·les 3 i 8 o 8 i 3 no són iguals: 

• a l'apartat 3, el fet de no demanar que l'última anella hagi de tenir al 50 sinó un nombre proper a ell, permet que els alumnes vagin provant i millorant les seves solucions sense sensació de fracàs mentre fan un munt de sumes que és en el fons el que volem practicar.

Aquesta proposta es pot complementar amb les #actrivitats "Cucs de Fibonacci" i "Cucs de Fibonacci acolorits" on es proposa aprofundir en patrons sobre els cucs com el comportament de la cinquena anella quan en les dues primeres hi ha nombres iguals o la distribució de les anelles que contenen nombres parells o senars.

https://innovamat.com/blog/ca/introduccio_actrivitats/

A alumnes més grans o com a tasca d'ampliació els podem preguntar quina relació troben entre l’anella central i la suma de les dels extrems (a la imatge següent es veu una justificació que pot complementar la conjectura que facin els alumnes al respecte)

Tasca 2

Però no cal restringir-nos a successions de 5 termes, aquí tenim un exemple proposat en Cicle Superior on l'objectiu és practicar de manera productiva el càlcul de mitjanes:

Quadern de Matemàtiques 6è (2015, Ed. Barcanova)

La justificació de que la mitjana entre la cel·les n i n+3 és la cel·la n+2 pot ser visual:

I també pot ser visual la justificació de que la mitjana entre la cel·les n, n+1 i n+6 és la cel·la n+4

Tasca 3

Comencem demanant que s'escriguin tots els termes de la successió de Fibonacci (en la seva versió estàndar, o sigui, començant amb 1 i 1) menors que 1000. Pot semblar una tasca molt llarga però ens adonem que no és així: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987

A continuació fem propostes com aquestes:

• verifica que entre aquests nombres només un de cada tres termes és parell, un de cada quatre és múltiple de 3, un de cada cinc és múltiple de 5. Com continuaries aquesta sèrie? 

• divideix cada terme de la successió entre 3 i pren nota dels residus que vas obtenint. Què observes? Què passa si canvies el divisor per un altre nombre (per exemple: 7)? 

Es pot veure que en dividir entre 3 els termes de la successió s'obtenen els residus: 1,1,2,0,2,2,1,0 en bucle. I aquests bucles es poden trobar qualsevol sigui el divisor. El @DavidKButlerUoA va piular imatges que il·lustren aquest fet amb reglets Cuisenaire. Per exemple, el cas del divisor 3:

@DavidKButlerUoA

La xifra final dels nombres que formen la successió de Fibonacci (o sigui, el residu de dividir aquests nombres entre 10) no s'escapen a aquest resultat i també es repeteixen seguint un bucle de longitud 60!! A més unint aquests nombres a mida que apareixen en el bucle es dibuixa un interessant patró geomètric, tal com es veu en aquesta imatge de @panlepan

@panlepan

• verifica la següent afirmació amb tots els nombres de dues xifres: "tot nombre natural es pot escriure de manera única com la suma de termes diferents de la successió de Fibonacci" 

Aquest resultat es coneix com a teorema de Zeckendorf i, a més afirma, que si exigim que no hagi nombres de Fibonacci consecutius la descomposció és única.

Els esquemes de Graham Fletcher

Fa uns dies, vam conèixer a través del sempre ben informat @druizaguilera aquesta sèrie de vídeos de @gfletchy que creiem que val la pena que recollim en un post ja que ens permeten reflexionar sobre la visió global que tenim sobre algunes temàtiques bàsiques de les matemàtiques en primària.

• inicis del comptatge 

Sobre aquest vídeo volem destacar l'ús que fa de les fitxes amb cares de dos colors per treballar les descomposicions dels dígits (minut 6:55)

• suma i resta

En aquest cas ens agraria destacar com utilitza la noció de "separar" per modelitzar la resta d'una manera que el portarà a fer transparent l'algoritme de la resta. (minut 4:50) 

• multiplicació 

Aquí destacarem l'ús que fa de la representació "pictòrica" com a pont entre el treball amb material manipulatiu i la representació simbòlica del treball fet amb el material (minut 3:40)

• divisió 

Deixant de banda que al final del vídeo dedica molt de temps a analitzar situacions que es fan més i més complexes a partir d'augmentar la quantitat de xifres del dividend i del divisor, que podria ser discutible, en aquest cas destaquem l'ús intensiu que fa del model rectangular de la multiplicació per recolzar els repartiments que involucren les divisions (minut 2:10)

• fraccions

A l'anàlisi que fa de l'estudi del significat, equivalència i comparació de fraccions destacarem la representació de fraccions sobre la línia numèrica des d'etapes molt més primerenques que les que acostumem a fer-ho per aquí.

Hi ha més informació sobre el treball de @gfletchy en el seu blog. Entre el seus posts destaquem especialment aquell en el que explica com es fan aquests vídeos.

Mondrian i la dissecció d'un quadrat en rectangles

Composició en vermell, groc, blau i negre
Oli sobre tela, 59.5x59.5, Piet Mondrian, 1921

Inspirant-se en l'obra de Mondrian MathPickle ens proposa aquest problema que ha estat un èxit cada vegada que l'hem portat a l'aula:

• Fes una graella de 10x10 
• Divideix la graella en rectangles diferents. ACLARIMENT: no es poden fer servir dos rectangles iguals, però sí que es poden fer servir dos rectangles diferents que tenen la mateixa àrea (per exemple, si hem utilitzat un rectangle de 2x3 no podem utilitzar un altre de 3x2 però sí un de 1x6).
• Acoloreix els rectangles seguint l’estètica del pintor Piet Mondrian. 
• Calcula la diferència entre el nombre de quadrets del rectangle més gran i el del més petit.

REPTE INICIAL: Quina és la diferència més petita que podeu aconseguir?

Els alumnes de 6è de @escolasadako van gaudir molt amb el problema, encara que cap d'ells va aconseguir la menor diferència possible (8).

La solució òptima de diferència 8 es pot obtenir així:

Però els alumnes de l'escola Tecnos de Terrassa, que es van entusiasmar moltíssim amb aquest problema, en conèixer aquesta solució es van proposar el repte de buscar-ne una altra que cap dels rectangles fos un quadrat. I no només ho van aconseguir sinó que ho van fer amb una solució més "elegant", utilitzant només sis rectangles!

Alguns mestres del seminari "Gràcia Barri Matemàtic" ho van proposar als seus alumnes de Cicle Mitjà i van explicar la seva experiència amb aquest problema al C2EM.

Els mestres del departament Col·laboratiu de Matemàtiques de la @FTrams també van proposar el problema als seus alumnes de Cicle Superior en el context del projecte Problemàtiques

Simon Gregg també va proposar aquest problema als seus alumnes:

ANEM MÉS ENLLÀ

• I si la graella inicial no és de 10x10 sinó de 4x4, 5x5, 6x6…?

El @druizaguilera ha representat així les solucions òptimes en aquests tres casos:

Així ho vam proposar als alumnes de 1r d'ESO de @escolasadako

MÉS REPTES

• És cert que a mesura que creix la mida de la graella inicial creix la solució òptima?
• És cert que si la graella inicial és de nxn, la solució òptima és menor o igual que n?

Podeu trobar un recull de solucions més informació sobre el problema aquí, aquí i aquí. En aquest últim enllaç trobareu aquest vídeo de Numberphile:




Al nostre blog tenim altres dos posts en els quals relacionem matemàtiques i art:

• en un d'ells analitzem els quadrats màgics que apareixen en les obres de Durer i Subirachs.
• en l'altre aprofitem les escultures d'Oldemberg per treballar la proporcionalitat geomètrica.

Pràctica productiva: restes (3)

A l'igual que Pràctica produtiva: restes (2) i a diferència de Pràctica produtiva: restes (1), la tasca sobre la que parlarem en aquest post forma part de l'article de @suma_fespm "Tareas ricas para practicar las restas"

Aquesta tasca està inspirada en el problema anomenat Diffy que ja vam comentar al post Pràctica productiva i pràctica reproductiva però amb una formulació diferent, més propera a l’estudi realitzat pel matemàtic E. Ducci en 1930 que va trobar que sense importar els nombres d’inici sempre s’arriba a quatre zeros (Font: Cut the knot)

Al "Cuaderno de Cultura Científica" la @MartaMachoS ha fet un article sobre "El teorema de Ducci" que ens ha permès conèixer una sèrie molt interessant de referències sobre aquest problema. Entre elles destaquem Carlos D’Andrea y Adrián Paenza, Un cuadrado, cuatro números, Pensamiento matemático vol VIII, no. 1, 71-82.

Farem diagrames amb les normes següents:

• en totes les files hi ha 4 cel·les en cada cel·la, 
• a partir de la segona fila, has d’escriure la diferència entre les dues cel·les que té immediatament a sobre 
• en el cas de l’última cel·la de cada fila la diferència l’has de fer entre el últim i el primer nombre de la fila anterior
• el diagrama acaba quan en tota la fila s’obtenen zeros

Exemple: començant amb els nombres 4, 1, 6 i 2 el diagrama té 5 files

En el context del projecte Problemàtiques alguns mestres del departament col·laboratiu de Matemàtiques de la @FTrams vam proposar a alumnes del cicle superior de Primària que triessin nombres de la primera fila perquè el diagrama tingués la major quantitat de files que puguessin aconseguir. L'activitat va ser un èxit, ja que va engrescar molt als alumnes.

A la següent imatge podeu veure l'anàlisi d'una alumna sobre com afecta l'ordre dels nombres de la primera fila a la quantitat de files del diagrama

En aquesta línia, alguns alumnes van voler analitzar totes les 24 possibles distribucions dels 4 nombres en la fila inicial, sense adonar-se que, per simetries i girs, en realitat només cal estudiar tres distribucions diferents i no més.

Els alumnes als que vam proposar el repte no van aconseguir diagrames de més de 8 files (val a dir que van trobar moltes quaternes diferents que generaven diagrames d’aquesta mida) possiblement perquè a partir de l'exemple, van creure que els nombres inicials havien de ser menors que 10.

El @rbalague11 ens va regalar aquest petit applet per experimentar amb diferents quaternes de dígits!!

Introdueix els quatre nombres inicials (entre 1 i 9)

Nombre de la posició 1:

Nombre de la posició 2:

Nombre de la posició 3:

Nombre de la posició 4:

Però el cert és que, si permetem que a les cel·les vagin nombres majors que 9, hi ha diagrames de tantes files com es vulgui. Per exemple:

• començant amb els nombres 1, 15, 30 i 60 el diagrama té 10 files
• començant amb els nombres 0, 653, 1854 i 4063 el diagrama té 24 files

Altres comentaris:

• Es pot preguntar quin és el diagrama en el que aconsegueixin que hi hagi nombres senars en major quantitat de files. El cert és que a partir de la cinquena fila mai queden nombres senars però es poden triar quaternes en que quedi algun senar fins a la 4a fila (per exemple: 2 4 6 7 → 2 2 1 5 → 0 1 4 5 → 1 3 1 3 → ...) Font: D. Shapiro
• Es pot proposar als alumnes que analitzin el joc quan en lloc de diagrames que tenen 4 nombres per fila en tenen altres quantitats. La conclusió de que sempre s’arriba a tots zeros pot deixar de ser certa Per exemple, per diagrames de 3 nombres per fila es pot entrar en un bucle 1 2 2 → 1 0 1 → 1 1 0 → 0 1 1 → 1 0 1 → 1 1 0 → 0 1 1... Acabem sempre amb el cicle aa0 → a0a → 0aa on a és el mcd dels nombres diferents de zero de la primera fila.
• Es pot demanar als alumnes que comparin un diagrama i el que resulta de sumar, restar o multiplicar a tots els nombres de la quaterna inicial per un mateix nombre.
• Don Steward proposa comprovar que si els 4 nombres inicials estan en progresió aritmètica la quantitat de files és sempre la mateixa (6), investigar què passa quan els 4 nombres inicials són quadrats consecutius, són nombres triangulars consecutius, són termes de Fibonacci, etc o estudiar què passa si a tots els nombres de la quaterna els multipliquem o els sumem un mateix nombre
• Es pot demanar als alumnes que per a la quaterna inicial triïn nombres que no siguin enters. En aquest sentit, a 4t d'ESO de @escolasadako, aquest any vam proposar als alumnos experimentar amb nombres irracionals

Val la pena analitzar que la petita quantitat de files també es dóna quan totes les entrades són irracionals. Aquí veiem l'anàlisi de la situació amb tres irracionals:

A la dreta apareixen les aproximacions decimals dels valors de cada cel·la per guiar la decisió de quin nombre és més gran i així decidir si es resta a-b o b-a.

El Josep, alumne del Màster de Secundària (grup 3, curs 18-19) ho va comprovar utilitzant els quatre irracionals més famosos

El Sergio B. (@magiaymates) es va preguntar: I per què no aplicar això per practicar restes de polinomis? Només haurem de decidir que vol dir fer la diferència entre dos polinomis...

A continuació apareix un exemple entenent que fer la diferència entre dos polinomis és fer la resta entre ells en l'ordre que permeti que el coeficient principal (el del terme de major grau) del resultat sigui positiu.

Els alumnes de #ESO4SDK (curs 18-19) van practicar la resta de polinomis amb aquesta tasca:

Una altra direcció d'ampliació d'aquesta tasca és l'estudi del mateix problema quan es canvia la quaterna inicial per una quíntupla: