Un itinerari de Mesura (1): massa

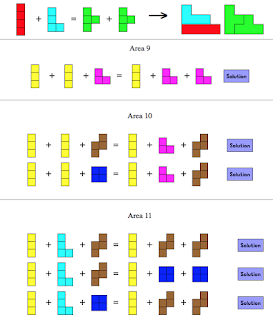
L'esquema de presentació de les activitats, és tret del llibre, que citem al final,  del Institut Freudenthal. Defineix tres moments per a introduir les diferents mesures:  

• comparar i ordenar (en el que es treballa el concepte)  
• ús d'unitats 
• ús d'instruments. 

Us presentem algunes activitats relacionades amb massa, organitzades seguint aquest esquema. Completant amb recursos que poden ajudar.

www.flickr.com

Comparar i ordenar

Comparar: sospesar dos objectes per comparar-los i veure quin és el que ens costa més d'aixecar porta implícit el concepte de mesurar masses. Una caixa plena de boles de porexpan o una plena de llibres mostra als alumnes més petits que la massa és una qualitat que no depèn necessàriament del volum.

Si els objectes a comparar són de massa semblant, segurament serà necessari agafar-los simultàniament un amb cada mà, amb els braços estesos, gairebé imitant una balança de plats.

La massa és una qualitat força abstracta. Fa molt temps algú ens va explicar com Decroly proposava la introducció del concepte de massa partint d'un seguit d'objectes quotidians. El primer que feien els alumnes era, utilitzant una balança de plats, equilibrar el pes de cadascun dels objectes amb sorra. Un cop fet, posaven la sorra en un mitjó, el tancaven i li penjaven una etiqueta amb el nom de l'objecte.
A partir d'aquí, preguntes usuals com: que pesa més l'estoig o la llibreta? quantes llibretes necessites per equilibrar el llibre? etc. es treballaven  utilitzant el mitjons prescindint dels objectes: Comparaven els mitjons amb les etiquetes corresponents en una balança.
Suposem que era una manera d'aïllar la idea de massa de l'objecte concret. Ens ho van explicar però no sabem si és cert. Si algú té referència d'això agrairem que ens ho indiqui en els comentaris.

Ordenar: per ordenar dues masses en tenim prou comparant directament els dos, com ens passa en el cas de la longitud.
No passa el mateix en el cas de voler ordenar més de dos objectes. En el cas de les longituds, ho fem de manera ràpida posant-les una al costat de l'altre formant escala (imaginem-ho amb els reglets), però ordenar més de dues masses precisa d'un treball sistemàtic molt interessant.
El el cas d'ordenar tres masses a,b, i c per exemple, haurem de seguir un procés com aquest.

• Agafar a i b, comparar
• Si a > b agafar b i c, comparar
• si b > c hem acabat: a > b > c
• si b < c ja sabem que b és el més lleuger dels tres però cal comparar a i b

Un cop han fet l'activitat, demanar que escriguin el procés que han seguit, o que escriguin les instruccions (algorismes) perquè una altra persona o un robot  ho pugui utilitzar amb la certesa que ho farà correctament  és una activitat molt interessant, que es pot estirar pels alumnes que tiben amb preguntes com:

• Tenim algun avantatge si en el tercer pas agafem a i c enlloc de b i c?
• Et veus en cor de fer l'esquema per quatre objectes? 

Una altra activitat interessant ens la ofereix el següent applet.

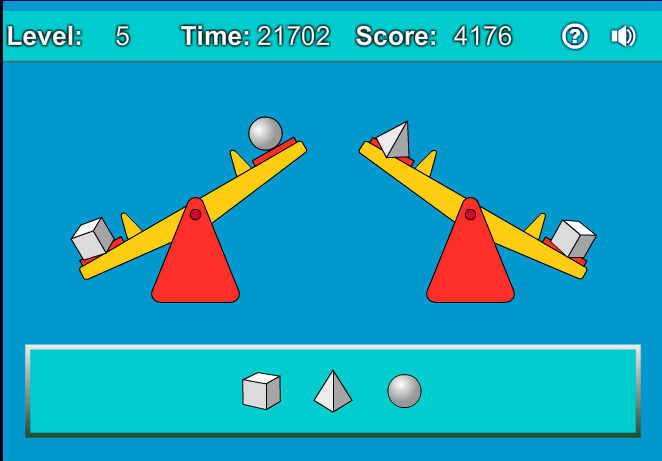http://appletspuntmat.blogspot.com.es/2014/04/mesura-balances-1.html

Demanar que escrigui "la història" d'una seqüència pot ser  una activitat molt rica. Es podria pensar que aquesta activitat entra a la categoria d'instruments, però no considerem les balances com a instrument fins que no entren en joc les unitats.

Unitats
Unitats arbitràries
Un pilot d'objectes iguals, per exemple bales de jugar, faciliten molt la tasca d'ordenar si disposem d'una balança de plats ja que identifiquem la massa amb un nombre, i és molt més eficaç a l'hora de comparar. Parlem amb els alumnes dels avantatges que representa disposar d'unitats.

 

Fins i tot els mateixos nens poden ser unitats de mesura (encara que no siguin iguals) un exemple el tenim en una activitat, plenament recomanable, de l'Institut Freudenthal, plantejada amb nens de quart a partir de la visita a un parc aquàtic: quants nens de classe pesen tant com un dofí?

Unitats estàndards
Com a unitat legal el quilo, amb el mig quilo o el quart de quilo, semblen els més adequats per començar, i un bric de llet com a substitut d'una pesa de quilo, un bon recurs.

No podem oblidar dedicar un temps a l'estimació del món que ens envolta amb preguntes com: quan pesa un nen de tres anys? i un pivot de la lliga de Bàsquet? en quins productes s'utilitzen els mil·ligrams? què és una tona? què es mesura amb tones? quants nens necessitaria per equilibrar la balança amb una tona? etc.

Entrant en el món de les "peses",Juan Garcia Moreno ens obsequia un cop més amb un dels seus fantàstics applets.

https://dl.dropboxusercontent.com/u/44162055/problem_retos_1/menuproblemitas.html
Per accedir-hi heu d'entrar a la pàgina, veureu una llista amb imatges i heu d'activar el de la balança

Instruments

Fer un recorregut pels diferents instruments de mesura pot ser una activitat culturalment interessant: les balances mecàniques, les romanes com a balances "portàtils" per mercats ambulats, el sistema de "peses",  ja desaparegut (didàcticament hi ha materials) poden ser les protagonistes de la classe durant uns dies.
A mig camí entre unitats i instruments el treball sobre les mesures tradicionals i els seus noms és molt gratificant, podem descobrir coses interessants, com per exemple, que el porró era una unitat de mesura. Veure informació aquí

Conversar sobre el quilo i de com solucionaven el problema que tots els quilos tinguessin la mateixa massa. L'existència del "cilindre model" en el Museu de mesures de París. L'equivalència entre quilo i litre d'aigua (amb certes condicions molt estrictes) com a model de referència, pot ser un descobriment apassionant pel nostres alumnes.

Altres aspectes: context per resoldre problemes
Molts cops la mesura de massa és utilitzada per plantejar problemes matemàtica recreativa, i que "enganxen als nostres alumnes" com per exemple:
Tenim 9 boles idèntiques, de les quals una és de diferent massa que les demés. Disposem d'un balança de plats. Esbrinar quina és la bola diferent, fent solament dues pesades.

http://nlvm.usu.edu/es/nav/frames_asid_139_g_4_t_2.html

D'altres és utilitzada com a context per plantejar problemes aritmètics.
Un exemple d'això el trobem a l'ARC (Creamat). Cal repartir el pes d'una compra de súper entre dos cistells, de manera que quedin equilibrats. Molt interessant la pregunta final, en la que demana que expliquin el mètode utilitzat. Va acompanyat d'un applet.

http://ares.cnice.mec.es/matematicasep/a/3/ca3_03.html

Comentaris finals

• L'esquema utilitzat en aquesta entrada (comparar i ordenar, ús d'unitats, ús d'instruments) està tret del llibre "Young Children Learn Measurement and Geometry" (2004).

• Podeu veure una explicació més detallada d'aquest tema a l'article "Algunas actividades para hablar de Medida" a la revista SUMA nº 77, dins de la secció "Ell@s tienen la palabra".

Matemàtiques per preparar el Nadal

Us proposem dues activitats que us poden donar l'oportunitat de guarnir la vostre classe amb motius nadalencs.

El Pep Bujosa ha fet un applet amb Geogebra per complementar aquesta proposta:

Cliqueu aquí per accedir a l'applet

Cliqueu aquí per veure una aplicació d'aquesta proposta al blog ORCA

Cliqueu aquí per veure treballs d'alumnes de 5è de Primària
de l'Escola Sadako en relació a aquesta tasca

Poliòminos i pensament exhaustiu

El mes passat vaig participar del VII CIBEM (Congreso Iberoamericano de Educación Matemática) a Montevideo. De les moltes activitats interessants en les que hi vaig poder participar (aquí n'hi ha un resum), vull aquí relatar un taller sobre poliòminos presentat per la Patricia Peralta i el José Salvador Carrasco de Bahia Blanca com a part de la sèrie sobre pensament exhaustiu que hem començat aquest curs

• Pensament exhaustiu
• Divisors i pensament exhaustiu 
• Geoplans i pensament exhaustiu

Van començar explicant que el terme poliòmino van ser inventat per Salomon Golomb i popularitzat per Martin Gardner

Després van definir els poliòminos com la unió de quadrats de la mateixa mida de manera que cada quadrat de la figura resultant ha de tenir un costat en comú amb un altre quadrat i a continuació van proposar als assistents que dibuixessin tots els tetròminos (poliòminos formats per 4 quadrats) possibles.

En aquest cas l'exhaustivitat requereix prendre decisions. Quina de les dues llistes és completa: la blava o la vermella?

Anomenaré a les peces blaves I, L, T, O i Z i a les peces vermelles I, L, L', T, O, Z i Z'

És interessant aquí fer notar el paper que hi juguen les experiències prèvies i l'ús de materials manipulatius: per persones que hagin jugat al Tetris com a videojoc (per exemple: aquí) la resposta és clarament la llista vermella, però per persones que hagin jugat a la versió de taula d'aquest joc, com que les peces materials permeten manipular-les, veuen innecessari duplicar les peces L, L', Z i Z'.

A continuació van proposar el problema de formar un rectangle amb totes les peces de la llista (ja sigui la vermella o la blava) i encara que va ser força ràpid que els assistents van decidir que era un problema impossible quedava per trobar una demostració d'aquesta impossibilitat. Van suggerir la demostració amb una imatge:

Si vull construir un rectangle amb les 5 peces, tindrà 20 quadrets d'àrea i si pinto aquest 20 quadrets com si fos un tauler d'escacs, 10 serien foscos i 10 serien clars. Tal com es veu a la imatge anterior les peces que he anomenat I, L, O i Z cobririen la mateixa quantitat de quadrets foscos i clars però la peça T no pot fer-ho i per tant amb les 5 peces és impossible construir un rectangle. L'argumentació per concloure que tampoc és possible fer-ho si afegim les peces L' i Z' és anàloga.

També vam treballar amb els llistats de tots els pentòminos i hexòminos. En els dos casos vam acordar treballar amb les listes curtes, o sigui, considerant iguals peces simètriques. 

En el cas dels 12 pentòminos vam veure que no només es podia construir un rectangle amb elles sinó que aquest rectangle no era únic.

commons.wikimedia.org

En el cas del 35 hexòminos van esmentar un altre problema que requereix exhaustivitat: trobar entre ells tots aquells que corresponen al desenvolupament del cub. Allí van esmentar les dificultats que troben els alumnes en aquesta tasca degut a la presència gaire bé exclusiva de desenvolupaments prototípicos en els llibres de text, en especial, el que apareix en el primer lloc de la segona fila en la següent imatge. 

Els 11 hexòminos que són desenvolupament d'un cub
commons.wikimedia.org

Comentaris posteriors:
Val la pena mirar aquest video del @eversalazar

Són molt interessant els problemetes de suma de poliòminos proposats per Erich Friedman:

https://erich-friedman.github.io/puzzle/polyadd/

També hem publicat una sèrie d'applets sobre aquest tema a Poliòminos

Bloc de matemàtiques 6-8

Acabem de publicar un bloc (dels de paper) de 96 activitats matemàtiques per a alumnes de 6 a 8 anys amb l'objectiu de fer-los pensar i divertir-se. Pot servir per a suggerir idees, passar l'estiu o incorporar activitats de cara a racons. Esperem que us agradi. Les activitats pertanyen a cinc aspectes diferents que van identificats amb una icona.

Exemples d'activitats

Compta quants nens, nenes, estels i pilotes hi ha en el dibuix i anota-ho en el requadre corresponent

Identifica les set diferències entre els dos dibuixos. Pensa que les diferències tenen a veure amb les matemàtiques.

Encercla el que veu el ninot en cada cas.

Llegeix amb atenció els enunciats i vés fent el que se’t demana.Treballaràs la simetria! 

(es tracta d'una mena d'encreuat en el que, com a guia, apareixen els eixos de simetria que té la lletra que va a cada requadre)

La Maria, la Paula, en Leo i en Lluís juguen a escacs.
Volen jugar tots contra tots. Podries ajudar-los a organitzar-se? Escriu les partides i els jugadors en el requadre.

Munta en les graelles com serien de dia les cases

amb els gomets que trobaràs al final del bloc.

Anna Cerezo, Cecilia Calvo, David Barba, Toni Benages:
"El bloc de MATES" Ed. Barcanova. ISBN: 978-84-489-3254-1

Quadrats màgics amb retenció de líquids

Dels 880 diferents quadrats màgics diferents de 4x4 aquesta setmana hem sabut a través de Futility Closet que molts retenen líquids.

Què volen dir amb això de retenir líquids?

Pensem en un quadrat màgic com una representació d'alçades d'una construcció feta amb cubets. Aquest tipus de representació la podem treballar amb l'applet Building with blocks que ja havíem presentat en l'entrada Visualització amb cubets però en aquesta ocasió fent servir l'opció Making height numbers.

Diuen que la construcció reté líquids si trobem alguna casella en la que, si "plou", les caselles que té al voltant, per les seves alçades, provocarien embassaments. En el cas de la imatge de l'esquerra (que òbviament no està relacionada amb quadrats màgics) no hi ha cap zona de la construcció on es retenguin líquids però si traduím a una costrucció amb cubets el quadrat màgic de Melancholia I d'Albrecht Dürer podem veure que "reté  líquid". 

En aquesta última imatge es pot "veure" que la construcció reté líquid a sobre de les torres d'altura 6 i 7

Intentem quantificar el líquid que queda embassat sobre les torres d'altura 6 i 7 (o el que és el mateix, entre les torres d'altura 10, 11, 12, 14, 15 i 9). Si prenem com a unitat de mesura el líquid que cap en una torre d'altura 1, com que l'embassament arribaria fins una altura de 9 (l'altura més baixa de les torres que l'envolten, a la imatge indicada amb groc), a sobre de la torre d'altura 6 es retenen 3 unitats de líquid i a sobre de la torre d'altura 7 se'n retenen 2, donant un total de 5 unitats de líquid embassat.

Això de retenir líquids no és inusual, segons Craig Knecht, 743 dels 880 quadrats màgics de 4x4 en retenen. El màxim que en poden retenir els quadrats màgics de 4x4 són 15 unitats i n'hi ha 12 solucions al problema de trobar els quadrats màgics que retenen aquesta quantitat de líquid:

Aquesta és una solució presentada per Hugo Pfoertner en el concurs 
Magic Water dels Al Zimmermann's Programming Contests

Aquestes altres dues solucions les hem pogut trobar entre el 

llistat de quadrats màgics de 4x4 associatius de la Wikipedia

Però a partir del llistat que apareix a l'informe final del concurs d'Al Zimmermann podem construir les altres 9 solucions.

Representem una solució fent servir Geogebra (en aquest cas la construcció
reté 6 unitats de líquid sobre la torre d'altura 3 i 9 unitats sobre la d'altura 2)

Representem una solució fent servir SketchUp (en aquest cas la construcció reté
5 unitats de líquid sobre la torre d'altura 4 i 10 unitats sobre la d'altura 1)

I aquí representem les restants set solucions

Matematiques anant pel carrer (5)

Comencem per un diari

Sota la bossa d'escombraries que hi ha posada al costat de la porta, a punt perquè la porti al contenidor, hi ha un full de diari per preservar el terra de possibles humitats no desitjades. Veig que els números de les dues pàgines (del mateix full) que estan cap a dalt són la 14 i la 35 i un seguit de preguntes em venen al cap:

1. Quins números estan a l'altre banda del full? 
2. Quantes pàgines té aquest diari? 
3. El número 20, on estarà: a la pàgina de la dreta o de l'esquerra? 
4. Quina serà la pàgina oposada de la 9? 
5. En algun moment el número de la pàgina de l'esquerra és més gran que la de la dreta?
6. Entre quines pàgines es veuen les grapes?
7. Quan sumen tots els números de pàgina del diari?

Les pàgines d'un llibre

Molts cops, quan s'acaba de llegir un llibre, ens trobem amb un dubte: per què hi ha una, dues o més pàgines blanques al final? quin paper juguen? serà per agafar apunts?

Tot té una raó. Ho hem preguntar a l'Enric, un amic que treballa en edició de llibres, i ens ho ha explicat. Cal dir que parlem de llibres cosits, no dels encolats. Un cop a casa per comprovar el que ens ha dit, agafem dos llibres de cuina: "Cuina per a solters" d'en Ismael Pardos i "El Gran Llibre de la Cuina Catalana" d'en Josep Lladonosa.

Comptem les pàgines que tenen en total aquests llibres, comptant també com a pàgines del llibre les blanques no numerades. El resultat és 192 i 720 respectivament. Si ara dividim el nombre de pàgines per 16, curiosament ens dóna un nombre enter, 192:16 = 12 i 720:16 = 45.
Això és degut a que per fer llibres cosits, en general, es fan "llibretes" (en diuen "plecs") de 16 pàgines o de 32 per després cosir-los. Per tant el nombre de pàgines d'un llibre per anar bé ha de ser múltiple de 16, i com que això és difícil de demanar als autors, complementen amb planes blanques. Proveu-ho amb algun dels vostres llibres. Molts llibres tenen un nombre total de pàgines múltiples de 16!
Us podeu trobar en que de vegades el quocient de la divisió no és enter (dóna 33,5 en el cas del llibre de Paul Auster "Creia que mi padre era Dios", per exemple). Això és degut a que arribar a un múltiple de 16 inclouria massa pàgines blanques i aleshores els editors  utilitzen un plec de 8 o fins i tot de 4 pàgines per "tancar el llibre."

Com és un plec?
Aquest és el model d'organització de les pàgines amb el que treballen a l'editorial de l'Enric

En aquest cas es tracta d'un plec de 32 pàgines. La mesura del full (16 impreses per les dues bandes)  si les pàgines del llibre fossin de mida DINA 4, és  un DIN A0, és dir un metre quadrat. Després cal plegar-lo i guillotinar-lo pels llocs indicats en vermell a la figura de la dreta, per a obtenir el plec.

Estudi d'un plec de 16 pàgines

Una bona activitat per portar a classe és construir un plec de de 16 fulls. Aquesta és la distribució de pàgines on a més de l'ordre s'indica el sentit del text de cada pàgina

Seguint aquest model, podem proposar als alumnes dividir un DINA4 en vuit rectangles iguals per cada banda, numerar els rectangles que representen les pàgines i construir el plec plegant-lo correctament.

Alguns aspectes per discutir: Tenint com a punt de partida la posició de la pàgina 1, la ubicació de les altres pàgines és un joc de simetries:

• darrera de l'1 ha d'anar el 2 però la direcció del text ha d'anar al revés. 
• al costat de l'1 ha d'anar el 16, perquè al plegar-les una sigui la pàgina inicial i l'altre la final

Descobrir que la suma de les pàgines que van de costat (1 i 16, 4 i 13, etc) és sempre la mateixa, és la clau de volta per resoldre l'activitat proposada. Si a més de construir el plec els fem escriure o explicar quines decisions han anat prenent per solucionar la tasca, aprofundirem molt més en el tema: "Que parlin ells"

Un joc de màgia plegant paper

Per acabar un joc de màgia que, com quasi sempre, hem après d'en Lluís Segarra.

• Feu dividir un full en 16 parts i escriure els nombres de l'1 al 16, en ordre (figura). Mentrestant escriu el nombre XXX en un paper i poseu-lo en un sobre.
• Feu doblegar el paper de la manera que vulguin (fent meitats, com un mapa, com un acordió...) fins que solament es vegi un dels rectangles numerats al davant.
• Retalleu els quatre costats de manera que els nombres us quedin solts, per poder-los utilitzar com a cartes.
• Separeu les cartes en dues piles: les que vinguin de cara les poseu en una pila i les que vinguin d'esquena en una altra.
• Demaneu a algú que sumi els nombres de la pila i digui en veu alta el resultat. Obriu el sobre i ensenyeu que aquest resultat coincideix amb el nombre que hi ha escrit (el nombre al que hem anomenat XXX). 

Quin és aquest nombre XXX que hauriem d'haver posat al sobre per tenir èxit en aquest joc? Serà realment "màgia"?

Vacances 3. Màgia Matemàtica

Si ens rebeu per mail, us demanem que cliqueu al títol per llegir directament el bloc: tindreu més informació i a més us podrem "comptar"

Les conferències TED són famoses tant per la categoria del seus  conferenciants com per la seva competència comunicativa. 

En aquests cicles de conferències les Matemàtiques també hi tenen cabuda. El cas que us presentem tracta d'una sessió de Màgia Matemàtica en la que el ponent, un gran calculista, sorprèn a l'auditori amb càlculs impossibles.

Moltes de les coses que fa són inabastables per mortals com nosaltres, però analitzant un dels trucs, hem trobat que qualsevol docent el podria repetir a classe o fer que els alumnes intentin esbrinar com s'ho fa. Us deixem amb el vídeo i posteriorment us plantegem el repte. Cal destacar que les conferències TED van acompanyades de l'opció  de poder accedir a subtítols, en espanyol gairebé sempre i en català algun dels cops, com és el cas d'aquest. Trobareu l'opció a la barra inferior.

Obert el 19/07/2011. en cas que no hi podeu accedir ens envieu un comentari a PuntMat.

El repte
Hi ha un moment del vídeo, aproximadament a partir del minut 5:50 i que ell mateix defineix com a un "petit truc", en que de quatre nombres que ha apuntat anteriorment que són nombres quadrats calculats mentalment en un repte anterior, planteja un nou repte:  quatre convidats han de multiplicar aquest nombre per un altre de de tres xifres, dir-li totes les xifres del resultat menys una i aleshores el mag endevina la que falta.

Quin truc fa servir? 

Esperem els vostres comentaris. Si obriu "comentaris" us trobareu una pregunta que us pot servir de primera pista, però si sou matemàtics de cor segurament no us ho mirareu. 

Un cop tingueu la solució, tant matemàtica com de la petita "trampa" que fa, ens l'envieu.

La curiositat
El que ens ha sorprès més d'en Arthur Benjamin és descobrir que en una altra intervenció en el mateix marc (aquest cop una comunicació curta) planteja com a solució alternativa a l'ensenyament de les Matemàtiques centrar bàsicament l'atenció en ...
Endevineu en que? Mireu el vídeo.

Es vol quedar sense feina, o vol eliminar la competència?