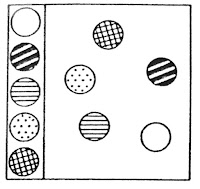
Es tracta d'una capseta de plàstic on hi ha una sèrie de boletes de diferents colors que apareixen alineades i no es poden moure i la mateixa quantitat de boles (i dels mateixos colors) que es mouen lliurement per la capseta. Al llibre "Combinatoire, statistiques et probabilités de 6 à 14 ans" de T. Varga i M. Dumont (1973) podem veure un dibuix i un petita anàlisi de l'artefacte i de les possibles coincidències quan alineem les boles lliures al costat de les fixes.
Comenten la temptació de pensar que la probabilitat de tenir k coincidències es representa així:
quan en realitat la probabilitat de que hi hagi 5 coincidència, malgrat que petita, és major que la probabilitat de que n'hi hagi 4, que és 0. Aquesta reflexió és extensible a altres quantitats de boles (n) ja que 1/n! = P(k=n) > P(k=n-1) = 0.
En realitat, la probabilitat de tenir k coincidències quan n= 5 es representa així:
En veure aquest gràfic ens ha sorprès que la diferència major en comparació al que proposàven Varga i Dumont com a "intuitiu" no és tant al voltant dels valors 4 i 5 com dels valors 0 i 1. Això es pot apreciar millor en analitzar la representació anterior per a altres quantitats de boles (n variant de 2 a 10)
 |
| Representació de la variació de la probabilitat de tenir k coincidències en els casos n=1 a n=10 |
- P(k=0) < P(k=1) quan n és senar i P(k=0) > P(k=1)
- la diferència entre les dues probabilitats és 1/n!
Aquestes conclusions deriven de les dades següents:
- A000166 llista de valors donada per l'OEIS per als desarranjaments, o sigui, permutacions en les quals cap dels elements del conjunt no apareix en la seva posició original
- A000240 llista de valors donada per l'OEIS per a les permutacions que tenen un únic element del conjunt que apareix en la seva posició original
- R(n,k) és el nombre de permutacions de n elements en què exactament k elements estan en les seves posicions originals (desarranjaments parcials).
 |
| Font: Perímetre |