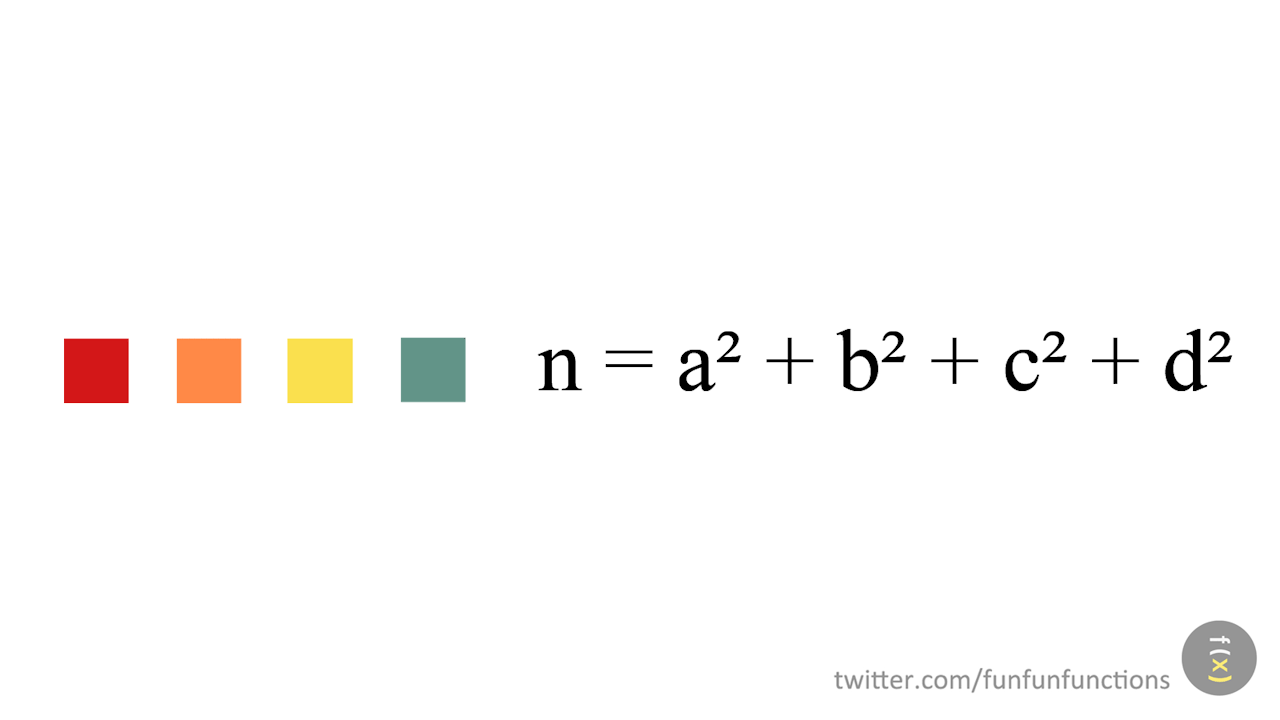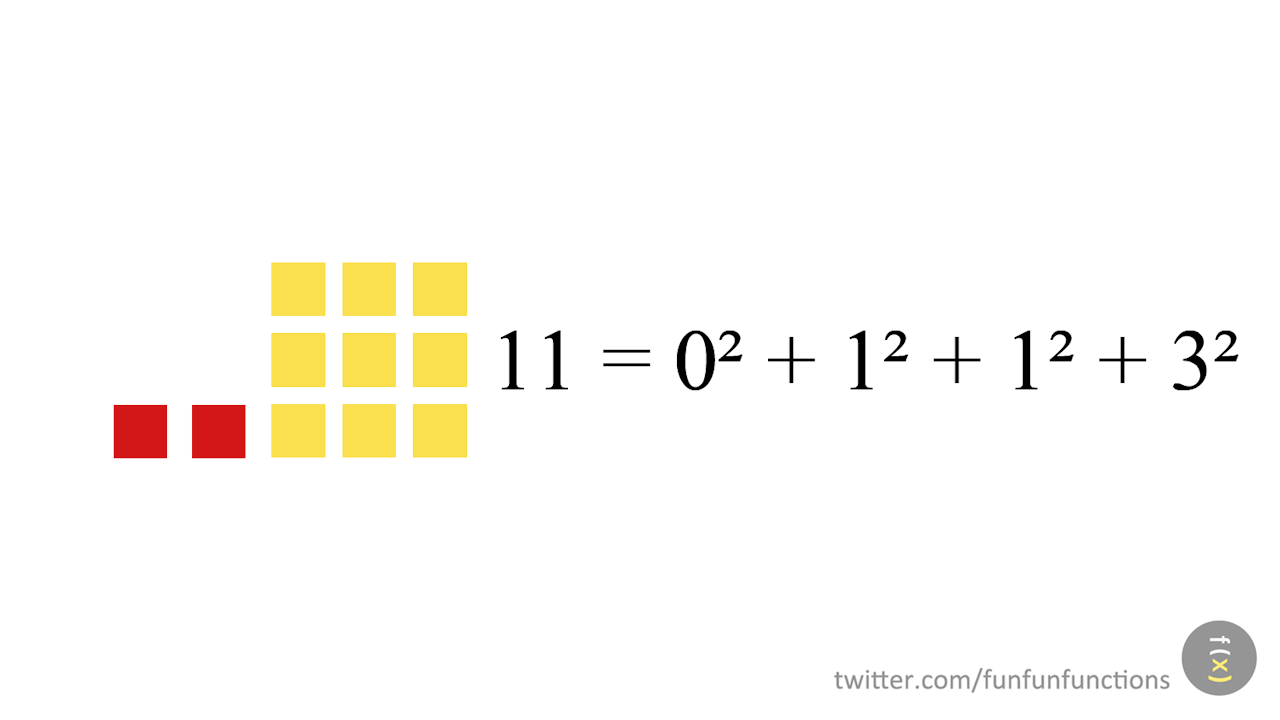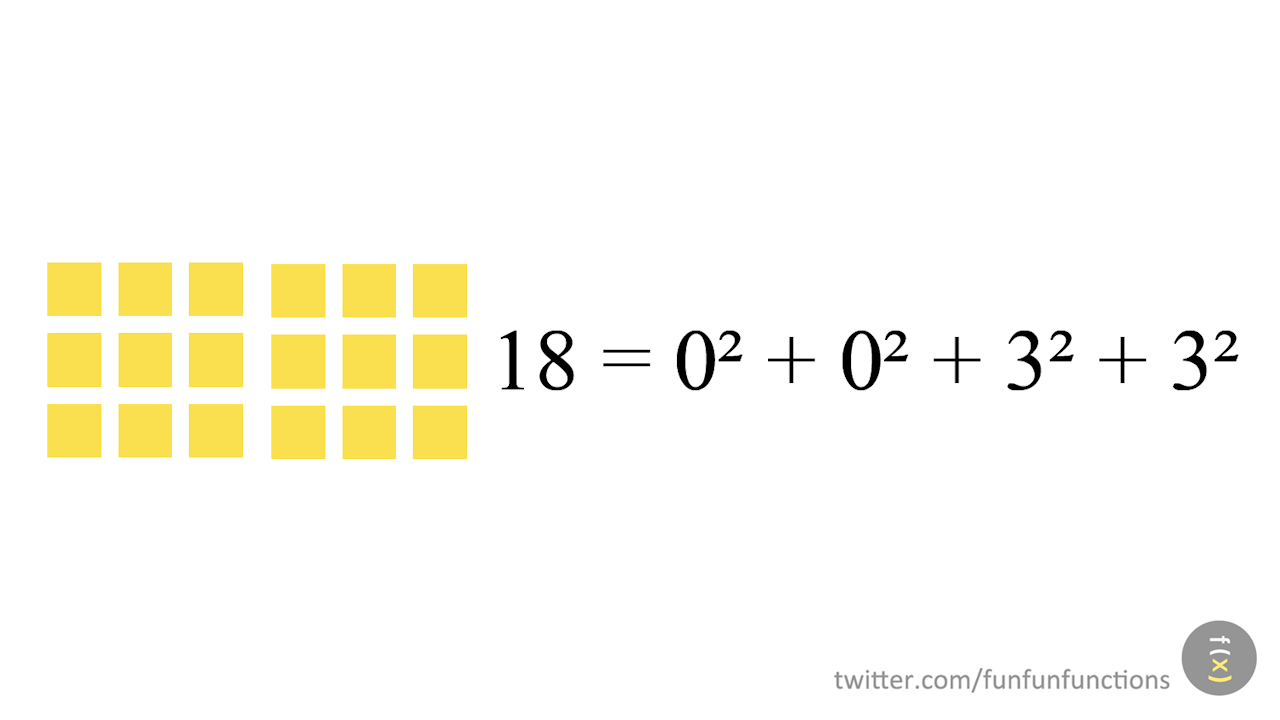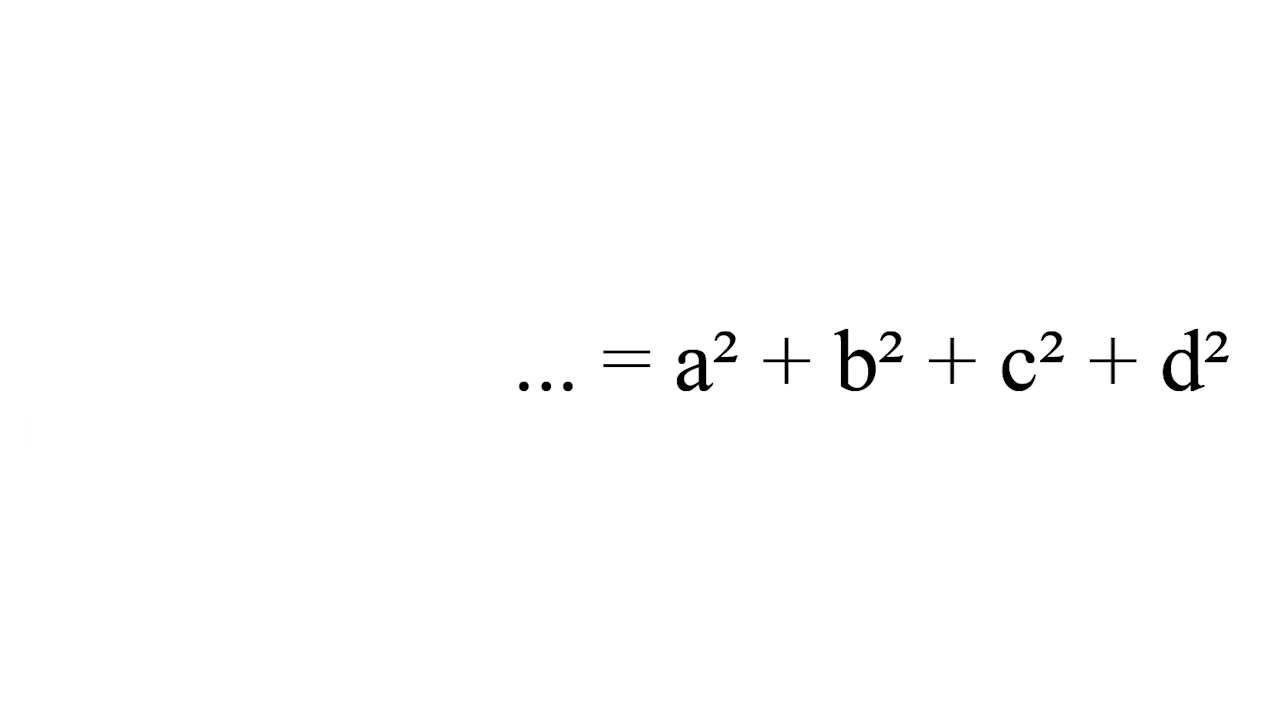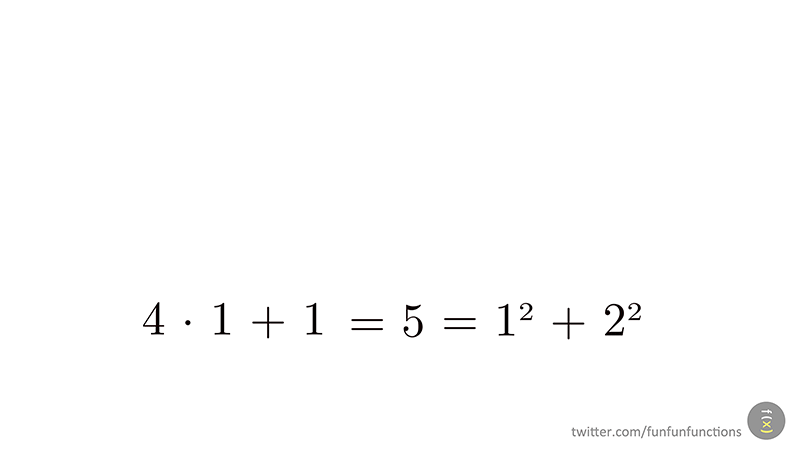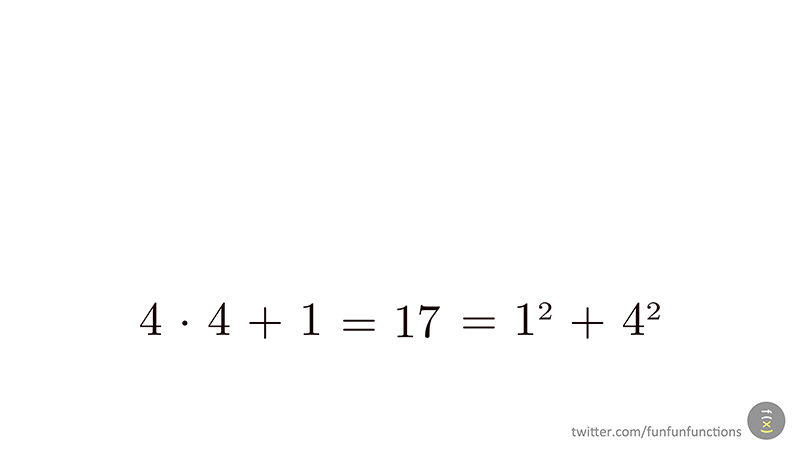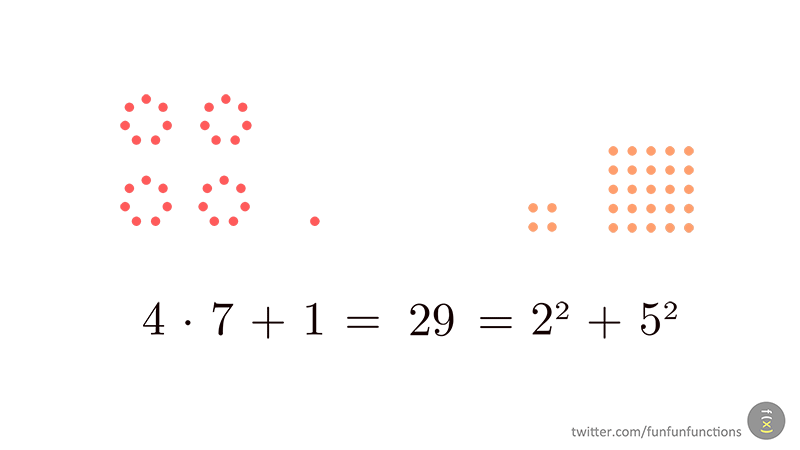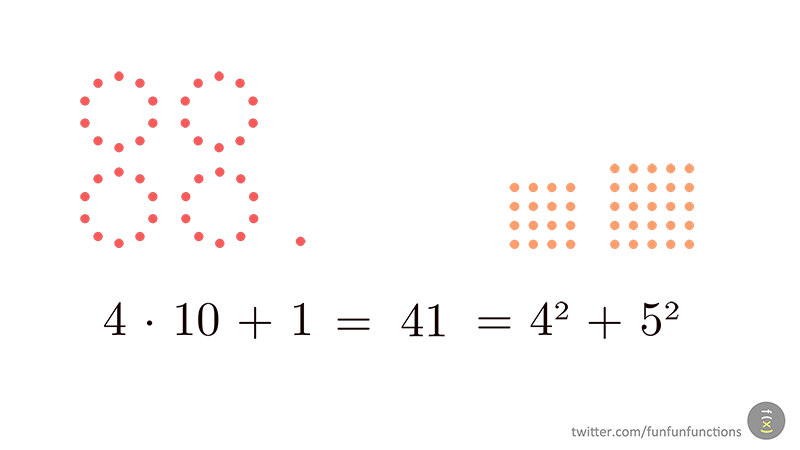Estem de celebració: el post anterior va ser el número 200, però també celebrem un aniversari: aquest curs fa 10 anys que vàrem publicar una col·lecció de quaderns d'Aritmètica seguint les idees dels holandesos de l'Institut Freudenthal en el seu llibre "Children Learn Mathematics".
El seu nom va ser 3x6.mat (sis cursos, tres quaderns per curs i el ".mat" que va donar origen al nostre nom "PuntMat"). Volia ser una proposta de llibre alternatiu d'Aritmètica des de primer a sisè. Actualment tot i que estan pràcticament descatalogats, (no és fàcil trobar-los) ens fa il·lusió pensar que ja fa 10 anys que estem parlant d'algorismes basats en nombres i no en xifres, flexibilitat al càlcul, models estructuradors (collarets, graella del 100, diners...), càlcul en columnes etc. i que poden ser un instrument útil, encara per gent que s'inicii en aquesta mentalitat.
Us convidem a una visita guiada en 18 "postals" (3 per curs) perquè tingueu una idea del seu contingut.
PRIMER DE PRIMÀRIA
Tipologia de problemes additius
 |
| Quadern 1 pàgina 23 |
Segons Carpenter, u
na de les classes de problemes additius són els de canvi (o transformació). L'activitat anterior és un exemple paradigmàtic d'aquest tipus de problemes, recrea un viatge d'autobús "Hi ha 9 persones en l'autobús, en baixen tres. Quantes queden a l'autobús? La proposta demana fer el problema manipulativament i l'objectiu és fer la transcripció simbòlica: identificar 9 - 3 = 6 amb "si n'hi van 9 i en baixen tres al final en queden 6". Més informació
aquí. Fins i tot hi ha vídeos que plategen problemes amb autobusos:
aqui
Comptatge acústic
 |
| Quadern 2 pàgina 11 |
Els tallerets són unes mini-activitats que encapsulen aproximadament la meitat de les pàgines dels quaderns de primer, curs en el que cal fer moltes activitats curtes d'adquisició d'habilitats
Dir l'anterior d'un nombre no és gens fàcil. Entre les primeres habilitats de comptatge hi ha el comptar endavant i endarrere d'un en un, i també la de dir l'anterior i el següent, habilitat que no és tan immediata com pot semblar a primera vista.
D'entrada algú que no hagi treballat amb nens i nenes d'aquestes edats veient que saben comptar endavant i endarrere, i que diuen el següent d'un nombre amb tota facilitat, pot pensar que si demana l'anterior passarà igual.
Si els fem fer l'activitat contestant sobre un paper no ens adonarem, però si els ho preguntem és molt possible que alguns nens tardin molt en donar la resposta. Si els demanem que diguin com ho compten per dir l'anterior de 13, veurem que el que fan és començar per l´ú anar fins el 13 i aleshores tirar endarrere i dir "12". Saber dir l'anterior és important sobretot quan els toqui solucionar problemes de resta.
La graella del 100
 |
| Quadern 3 pàgina4 |
La graella del 100, un dels recursos molt utilitzats en aquests quaderns ja que es aacompanya a identificar unitats i desenes de manera estructurada, a CI, a estudiar els múltiples a CS, passant per les multiplicacions a CM.
En aquesta activitat, es treballen dos aspectes: escriure l'anterior i el següent d'un nombre i trobar quin nombre va a cada color.
Les estratègies per solucionar la segona part de la tasca poden ser diverses: per exemple, per fer el requadre vermell, poden partir del 49 i fer 49 i 59, 69 i després dir l'anterior: 68 o poden sortir del 75 i fe 65,66 etc del 30 etc. L'objectiu de càlcul és treballar el comptatge acústic d'un en un i de deu en 10 endavant i endarrere. Més informació
aquí i
aquí.
SEGÒN DE PRIMÀRIA
Pràctica individual d'habilitats
 |
| Quadern 4 pàgina2 |
L'objectiu d'aquest tipus d'activitat és Informar als alumnes i als seus pares sobre el què es treballarà de pràctica. Això permet que els alumnes s'assabentin que els va bé i en que van més fluixos.
Aquest tipus d'activitats surten dos cops a cada quadern, de primer a tercer curs, a la pàgina 2 i 14. Això implica que funciona com a avaluació inicial o presentació de continguts, en començar i quan s'està a la meitat del quadern.
La línia numèrica buida
 |
| Quadern 5 pàgina 4 |
L'ús de models estructurats com la recta numèrica ens permet, treballar habilitats bàsiques: comptar de 10 en 10 i de 5 en 5, estratègies de càlcul per exemple per arribar a 59 poden fer cinc salts de 10, un de 5 i quatre d'1, però també sis salts de 10 i tirar enrere un. Aquesta és l'anomenada estratègia de salts que permet "fer sumes" amb altres instruments que no siguin els algorismes. Més informació
aquí.
Estimació
 |
| Quadern 6 pàgina 5 |
Tenim aquí un exemple d'activitat en la que el càlcul mental ve acompanyat de certa capacitat de decisió. Per exemple, per decidir si 59+41 és més gran, igual o més petit que 100 cal afinar, però amb 34+30 no cal fer la suma. Amb quines parelles de nombres passaria això? per què? i en les restes?. Més informació
aquí.
TERCER DE PRIMÀRIA
Les taules de multiplicar
 |
| Quadern 7 pàgina 10 |
Si durant el procès d'aprenentatge de les taules de multiplicar, ens fixem en les tècniques de memorització que utilitzen de manera natural els alumnes que avancen més, veurem que molts cops apliquen una estratègia que anomenem "fets coneguts - fets derivats". Si partim que els alumnes ja saben la taula del 10 i han de calcular 7x9, per exemple, poden pensar si 10 grups de 7 són 70, nou grups seran 70-7. Raonaments com aquests els obra la porta a seva memorització. Més informació sobre taules
aquí,
aquí,
aquí i
aquí.
 |
| Quadern 8 pàgina 6 |
A partir de dos personatges es discuteix la confrontació entre les seves (als que podríem anomenar l’algorísmic i el "gandul"), o sigui el que busca la manera més eficaç de fer-ho per promoure l'ús d'estratègies alternatives eficients. Per poder fer el gandul, cal dominar les Mates.
Propostes als pares i mares
 |
| Quadern 9 pàgina 2 |
Convidar als pares i mares a fer activitats que no representin "ensenyar-los res" sinó plantejar reptes, que molts cops tenen la particularitat que impliquen a tota la família, des del punt de vista que d'entrada ningú té la solució.
En aquest cas es tracta de triar, entre les cartes de l'1 al 9 quatre nombres i utilitzant-los tots quatre, sumant restant multiplicant o dividint aconseguir el nombre 24.. Per exemple amb 1,2, 3 i 4 una solució podria ser 3x4x2x1, i amb 2,3,5 i 7, 7x3+5-2. Ideal per a un viatge avorrit en cotxe: apuntar la matricula del cotxe del davant i mirar d'aconseguir el 24 amb els seus 4 nombres, a veure qui dels viatgers ho troba.
QUART DE PRIMÀRIA
Construcció dels algorismes
 |
| Quadern 10 pàgina 24 |
Ens els últims quatre anys s'ha parlat molt del fet de portar a les classes els algorismes basats en nombres, com a un contingut més a treballar, endarrerint la presentació dels algorismes estàndard. En relació a això, en el plantejament del 3x6.mat optem per el "càlcul en columnes". La proposta és que tots els alumnes dominin aquest tipus d'algorisme i endarrerir la presentació dels estàndard. Aquest full és la introducció a la divisió en columnes.
La il·lustració que acompanya a l'explicació no és gratuïta: la construcció grupal ajuda a la transparència, es a dir a entendre a fons cada pas que realitzen. Podeu trobar més informació sobre el tema de la construcció
aquí
Pràctica productiva
 |
| Quadern 11 pàgina 25 |
A l'hora de exercitar algorismes, normalment s'acostumen a proporcionar fulls d'operacions, activitats que tenen una dinàmica passiva. En plantejar un treball en grup en el que cal resoldre un "problema" com l'anterior, fer divisions forma part del procès: Però no és l'objectiu. L'objectiu és resoldre el repte.
Si demanem al final si han fet servir alguna estratègia, poden sortir respostes com, en el cas del 723, per exemple, "provo primer amb el 7 al divisor ja que amb el 2 solament pot ser l'1 o el 2.
Més informació sobre aquesta activitat en concret
aquí
Minilliçons
 |
| Quadern 12 pàgina 30 |
Minilliçons són aquelles activitats que promouen l'ús de fets derivats: deduir el resultat d'una operació a partir d'una ja resolta. Implica entrar a manejar propietats de les operacions, sentit numèric, etc. i així aprofundir en el coneixement dels nombres, les seves propietats i les estratègies implicades.
S'avisa amb un llamp quan l'exercici és complicat. Activitats així potencíen "que parlin ells" quan han d'explicitar el raonament que els ha portat a solucionar la tasca.
CINQUÈ DE PRIMÀRIA
Acotar i estimar
 |
| Quadern 13 pàgina 30 |
En aquesta activitat, un altre cop, el "que parlin ells" es potencia. Per exemple: en el cas del 439x3:
- "Arrodonint per baix 400x3= 1200 per tant serà més gran que 1200"
- "arrodonint a per dalt 132 x 5 farem 200x5 = 1000.
- Per tant 132x5 serà la més petita. Ho comprovem amb la calculadora
Calculadora trencada
 |
| Quadern 14 pàgina 12 |
Sota aquest nom hi entra un tipus d'activitats en la que l'argument principal és que disposem d'una calculadora que té algunes tecles que no funcionen. Això genera el problema que per calcular una operació, necessito trobar un camí alternatiu. Com resoldre el problema?
Per exemple en el cas de 36 x 374 una sortida seria multiplicar per 18 i per 2, o per 72 i dividir per dos, o multiplicar per 35 y sumar 374.
Trobareu informació
aquí. Val a dir que en aquest cas els applets ens fan un gran servei i hi ha un bon recull d'aquest tipus de calculadores al nostre
blog d'applets.
Ús del context
divisió amb decimals
 |
| Quadern 15 pàgina 31 | |
La presentació de continguts o procediments nous en cursos elevat, es continua plantejant sota la filosofia del "càlcul en context", és a dir plantejar una activitat que els alumnes puguin resoldre, aplicant els seus coneixement, dona una base sòlida per posteriorment passar al món del símbols.
En aquest cas el contingut a treballar és "treure decimals en una divisió" on enlloc de explicar quan i com posar la coma, es comença per resoldre una situació en context: repartir 10€ entre 4 moneders manipulativament veure que dóna 2€ i 50 cèntims: 10:4=2,50, i a partir d'aquí s'anirá avançat progressivament cap el camp simbòlic, a psrtir de converses a classe.
SISÈ DE PRIMÀRIA
Càlcul ràpid
 |
| Quadern 16 pàgina 30 |
Les sèries de càlcul ràpid, com per exemple les del Quinzet, presenten l'avantatge que es realitzen una quantitat important d'operacions en un període de temps curt: Es centren en càlculs bàsics i taules de multiplicar o "de dividir".
En el 3x6.mat, es presenten en dos fulls per quadern, a l'apartat d'avaluació, amb un canvi important: augmenta la mida dels nombres, proposant operacions com, per exemple, 341+104 o divisions tipus 12:5, en les que cal donar quocient i residu.
A sisè els dos fulls es diferencien. El primer, que segueix la idea de cinquè es titula "Rapidesa d'operacions: les de sempre" i l'altre, "Rapidesa d'operacions: coses noves" on s'amplia el camp i es fan: sèries de fraccions d'una quantitat, divisibilitat, tants per cent, sumes i restes de fraccions senzilles, trobar fraccions equivalents, divisibilitat, ordenar fraccions, ordenar decimals etc
Algorismes històrics
 |
| Quadern 17 pàgina 24 |
Hi ha una idea generalitzada sobre el caràcter únic de l'algorisme amb el que es resolen els càlculs aritmètics. Però es tracta d'una idea equivocada, els algorismes varien segons el lloc i l'època. Pel que fa al lloc, un exemple molt proper el tenim en la resta portant-ne, en el que molta gent afegeix les que es porten en el subtrahend, mentre que a la majoria de països la treuen del minuend. L'algorisme de la multiplicació a Cuba o Alemanya és diferent al que utilitzem en el nostre país, un exemple el trobareu
aquí.
Pel que fa a l'època, en els quaderns hem recollit algun exemple d'algorismes antics per posar de manifest aquest fet
Per més informació podeu consultar "Barba, D. Calvo,C: Algoritmos antiguos de càlculo. Cuadermos de pedagogia 421, març 2012
Explicitar processos
La figura del robot és utilitzada per a promoure activitats de comunicació: el robot és molt útil, però no pren decisions. necessita que li escriguin les instruccions precises perquè faci de manera correcta el que se li demana. Per tant cal "afinar molt" les instruccions. Creiem que és un bon aliat per que parlin ell@s, i va apareixent de volta en quan en algunes pàgines.
Comiat
Esperem que aquestes 18 postals us hagin acostat a aquest país nostre anomenat 3x6.mat. Qualsevol comentari o aportació ens ajudarà a tancar aquest desé l'aniversari