El mes passat vaig participar del VII CIBEM (Congreso Iberoamericano de Educación Matemática) a Montevideo. De les moltes activitats interessants en les que hi vaig poder participar (aquí n'hi ha un resum), vull aquí relatar un taller sobre poliòminos presentat per la Patricia Peralta i el José Salvador Carrasco de Bahia Blanca com a part de la sèrie sobre pensament exhaustiu que hem començat aquest curs
Van començar explicant que el terme poliòmino van ser inventat per Salomon Golomb i popularitzat per Martin Gardner
Després van definir els poliòminos com la unió de quadrats de la mateixa mida de manera que cada quadrat de la figura resultant ha de tenir un costat en comú amb un altre quadrat i a continuació van proposar als assistents que dibuixessin tots els tetròminos (poliòminos formats per 4 quadrats) possibles.
En aquest cas l'exhaustivitat requereix prendre decisions. Quina de les dues llistes és completa: la blava o la vermella?
 |
| Anomenaré a les peces blaves I, L, T, O i Z i a les peces vermelles I, L, L', T, O, Z i Z' |
És interessant aquí fer notar el paper que hi juguen les experiències prèvies i l'ús de materials manipulatius: per persones que hagin jugat al Tetris com a videojoc (per exemple: aquí) la resposta és clarament la llista vermella, però per persones que hagin jugat a la versió de taula d'aquest joc, com que les peces materials permeten manipular-les, veuen innecessari duplicar les peces L, L', Z i Z'.
A continuació van proposar el problema de formar un rectangle amb totes les peces de la llista (ja sigui la vermella o la blava) i encara que va ser força ràpid que els assistents van decidir que era un problema impossible quedava per trobar una demostració d'aquesta impossibilitat. Van suggerir la demostració amb una imatge:
Si vull construir un rectangle amb les 5 peces, tindrà 20 quadrets d'àrea i si pinto aquest 20 quadrets com si fos un tauler d'escacs, 10 serien foscos i 10 serien clars. Tal com es veu a la imatge anterior les peces que he anomenat I, L, O i Z cobririen la mateixa quantitat de quadrets foscos i clars però la peça T no pot fer-ho i per tant amb les 5 peces és impossible construir un rectangle. L'argumentació per concloure que tampoc és possible fer-ho si afegim les peces L' i Z' és anàloga.
També vam treballar amb els llistats de tots els pentòminos i hexòminos. En els dos casos vam acordar treballar amb les listes curtes, o sigui, considerant iguals peces simètriques.
En el cas dels 12 pentòminos vam veure que no només es podia construir un rectangle amb elles sinó que aquest rectangle no era únic.
 |
| commons.wikimedia.org |
En el cas del 35 hexòminos van esmentar un altre problema que requereix exhaustivitat: trobar entre ells tots aquells que corresponen al desenvolupament del cub. Allí van esmentar les dificultats que troben els alumnes en aquesta tasca degut a la presència gaire bé exclusiva de desenvolupaments prototípicos en els llibres de text, en especial, el que apareix en el primer lloc de la segona fila en la següent imatge.
| Els 11 hexòminos que són desenvolupament d'un cub commons.wikimedia.org |
Val la pena mirar aquest video del @eversalazar
Són molt interessant els problemetes de suma de poliòminos proposats per Erich Friedman:
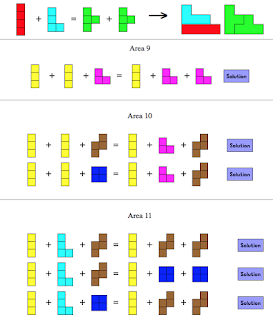 |
| https://erich-friedman.github.io/puzzle/polyadd/ |
També hem publicat una sèrie d'applets sobre aquest tema a Poliòminos

Per jugar amb poliominos http://www2.stetson.edu/~efriedma/polyadd/
ResponEliminaEnllaç actualitzat
Eliminahttps://erich-friedman.github.io/puzzle/polyadd/
Per estudiar quins pentaminos tesselen el pla:
ResponEliminahttp://donsteward.blogspot.com.es/2013/12/tessellations.html