- Enganxa entre si, de totes les maneres possibles, les tres peces per obtenir una figura amb un eix de simetria
Quan vam proposar aquesta tasca a alumnes de 2n d'ESO van trobar de molta ajuda construir-se les peces pra manipular-les, però de tota manera havíen de registrar les solucions trobades sobre paper.
- Enganxa entre si, de totes les maneres possibles, les tres peces per obtenir una figura amb un eix de simetria
- Enganxa entre si, de totes les maneres possibles, les tres peces per obtenir una figura amb un eix de simetria
Durant les sessions de febrer de 2018 del seminari "Gràcia, barri matemàtic" treballant aquest problema vam observar que en tots els casos l'eix de simetria travessava una quantitat senar de quadrets i sempre travessava la peça taronja. Aquestes propietats ens van ajudar a millorar la solució que teniem, fins aconseguir 14 figures simètriques:
També vam discutir ventatges i inconvenients de que les tres peces tinguin colors diferents en contrast a com seria l'activitat si les tres peces fossin del mateix color.
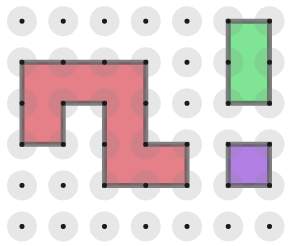
En cas que no s'exigeixi que les peces han de compartir un costat s'afegeixen altres solucions, com per exemple:
Els alumnes van trobar unes quantes d'aquestes solucions:
- Enganxa entre si, de totes les maneres possibles, les tres peces per obtenir una figura amb un eix de simetria
En el blog ORCA es pot veure com els fills de la Marleen van trobar aquestes solucions fent servir peces de Lego
En el Reflecting Squarely del projecte Nrich també trobem un problema d'aquest tipus amb les peces:
Allí es deixa molt clar que les peces s'han d'enganxar de manera que els vèrtxes de les tres figures han de ser punts de la graella i el contacte entre les peces no pot ser només el vèrtex. En aquestes condicions les solucions són nou. Trobem molt interessant les tasques d'ampliació que s'hi proposen:
- Dissenya altres tres figures (la suma de les tres àrees no hauria de superar 10 quadradets) i calcula la quantitat de maneres en es poden disposar per fer formes simètriques
- Pots trobar tres figures que donin lloc a més solucions que el cas original?
- Pots trobar tres figures per a les quals no hi hagi solució?
En la XXI jornada de l'ABEAM van recollir dos nous puzles de simetria proposats pel @MMACA_cat. L'objectiu en cada cas és el mateix: juxtaposant les peces, sense sobreposar-les, aconseguir un polígon (sense forats) amb un eix de simetria:
Cap comentari:
Publica un comentari a l'entrada